摘要:(三)证明题 1.略 2.证ED是直径,∵AD平分∠BAC,∴BD=CD 结论成立. 3.连MB,证∠BMC=∠DMB.
网址:http://m.1010jiajiao.com/timu3_id_450227[举报]
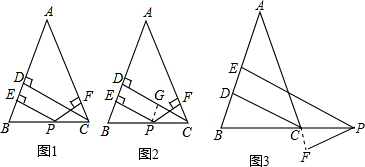
请看下面小明同学完成的一道证明题的思路:如图1,已知△ABC中,AB=AC,CD⊥AB,垂足是D,P是BC边上任意一点,PE⊥AB,PF⊥AC,垂足分别是E、F.
求证:PE+PF=CD.
证明思路:
如图2,过点P作PG∥AB交CD于G,则四边形PGDE为矩形,PE=GD;又可证△PGC≌△CFP,则PF=CG;所以PE+PF=DG+GC=DC.若P是BC延长线上任意一点,其它条件不变,则PE、PF与CD有何关系?请你写出结论并完成证明过程. 查看习题详情和答案>>
查看习题详情和答案>>
求证:PE+PF=CD.
证明思路:
如图2,过点P作PG∥AB交CD于G,则四边形PGDE为矩形,PE=GD;又可证△PGC≌△CFP,则PF=CG;所以PE+PF=DG+GC=DC.若P是BC延长线上任意一点,其它条件不变,则PE、PF与CD有何关系?请你写出结论并完成证明过程.
 查看习题详情和答案>>
查看习题详情和答案>>
为了使同学们更好地解答本题,我们提供了思路点拨,你可以依照这个思路填空,并完成本题解答的全过程,当然你也可以不填空,只需按照解答的一般要求,进行解答即可。
如图,已知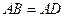 ,
,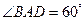 ,
,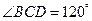 ,延长
,延长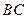 ,使
,使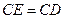 ,连结
,连结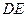 ,求证:
,求证: .
.
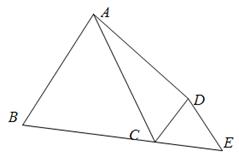
思路点拨:
【小题1】⑴由已知条件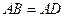 ,
,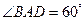 ,可知:
,可知: 是 三角形;
是 三角形;
【小题2】⑵同理由已知条件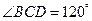 得到
得到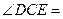 ,且
,且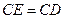 ,可知 ;
,可知 ;
【小题3】⑶要证 ,可将问题转化为两条线段相等,即 =" " ;
,可将问题转化为两条线段相等,即 =" " ;
【小题4】⑷要证(3)中所填写的两条线段相等,可以先证明….请你完成证明过程: 查看习题详情和答案>>
如图,已知
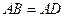 ,
,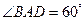 ,
,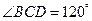 ,延长
,延长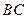 ,使
,使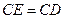 ,连结
,连结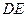 ,求证:
,求证: .
.
思路点拨:
【小题1】⑴由已知条件
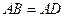 ,
,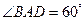 ,可知:
,可知: 是 三角形;
是 三角形;【小题2】⑵同理由已知条件
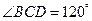 得到
得到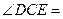 ,且
,且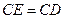 ,可知 ;
,可知 ;【小题3】⑶要证
 ,可将问题转化为两条线段相等,即 =" " ;
,可将问题转化为两条线段相等,即 =" " ;【小题4】⑷要证(3)中所填写的两条线段相等,可以先证明….请你完成证明过程: 查看习题详情和答案>>
为了使同学们更好地解答本题,我们提供了思路点拨,你可以依照这个思路填空,并完成本题解答的全过程,当然你也可以不填空,只需按照解答的一般要求,进行解答即可。
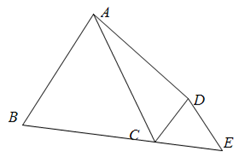
如图,已知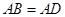 ,
,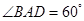 ,
,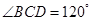 ,延长
,延长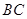 ,使
,使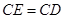 ,连结
,连结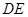 ,求证:
,求证: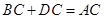 .
.
思路点拨:
【小题1】⑴由已知条件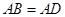 ,
,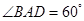 ,可知:
,可知: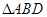 是 三角形;
是 三角形;
【小题2】⑵同理由已知条件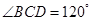 得到
得到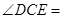 ,且
,且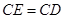 ,可知 ;
,可知 ;
【小题3】⑶要证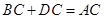 ,可将问题转化为两条线段相等,即 = ;
,可将问题转化为两条线段相等,即 = ;
【小题4】⑷要证(3)中所填写的两条线段相等,可以先证明….请你完成证明过程: