题目内容
圆的切线
[1]定义:和圆有
[2]判定:(1)到圆心的距离等于这个圆的
(2)经过半径
[3]性质:(1)圆的切线
(2)从圆外一点引圆的两条切线,它们的切线长
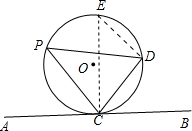
结论:P是⊙O外一点,PA、PB分别切⊙O于A、B,C是弧AB上一点,DE切⊙O于C交PA、PB于D、E,则△PDE的周长为
[1]定义:和圆有
一个交点
一个交点
的直线叫圆的切线.[2]判定:(1)到圆心的距离等于这个圆的
半径
半径
的直线是圆的切线;(2)经过半径
的外端
的外端
并且垂直于
垂直于
这条半径的直线是圆的切线.[3]性质:(1)圆的切线
垂直于
垂直于
过切点
切点
的半径.(2)从圆外一点引圆的两条切线,它们的切线长
相等
相等
,圆心和这个点的连线平分两切线的夹角
两切线的夹角
.(切线长定理)结论:P是⊙O外一点,PA、PB分别切⊙O于A、B,C是弧AB上一点,DE切⊙O于C交PA、PB于D、E,则△PDE的周长为
2PA
2PA
.分析:[1]根据切线的定义得出即可;
[2]根据切线的判定得出即可;
[3]根据切线的性质和切线长定理得出即可;
结论:根据切线长定理得出PA=PB,DA=DC,EC=BE,即可求出答案.
[2]根据切线的判定得出即可;
[3]根据切线的性质和切线长定理得出即可;
结论:根据切线长定理得出PA=PB,DA=DC,EC=BE,即可求出答案.
解答:解:[1]定义:和圆有一个交点的直线叫圆的切线,
故答案为:一个交点;
[2]判定:(1)到圆心的距离等于这个圆的半径的直线是圆的切线;
(2)经过半径的外端并且垂直于这条半径的直线是圆的切线;
故答案为:半径,的外端,垂直于;
[3]性质:(1)圆的切线垂直于过切点的半径,
(2)从圆外一点引圆的两条切线,它们的切线长相等,圆心和这个点的连线平分两切线的夹角,
故答案为:垂直于,切点,相等,两切线的夹角;
结论:
∵PA、PB分别切⊙O于A、B,DE切⊙O于C,
∴PA=PB,DA=DC,EC=BE,
∴△PDE的周长是PD+DE+PE=PD+DC+CE+PE=PD+AD+BE+PE=PA+PB=2PA,
故答案为:2PA.
故答案为:一个交点;
[2]判定:(1)到圆心的距离等于这个圆的半径的直线是圆的切线;
(2)经过半径的外端并且垂直于这条半径的直线是圆的切线;
故答案为:半径,的外端,垂直于;
[3]性质:(1)圆的切线垂直于过切点的半径,
(2)从圆外一点引圆的两条切线,它们的切线长相等,圆心和这个点的连线平分两切线的夹角,
故答案为:垂直于,切点,相等,两切线的夹角;
结论:

∵PA、PB分别切⊙O于A、B,DE切⊙O于C,
∴PA=PB,DA=DC,EC=BE,
∴△PDE的周长是PD+DE+PE=PD+DC+CE+PE=PD+AD+BE+PE=PA+PB=2PA,
故答案为:2PA.
点评:此题综合运用了切线的性质定理、判定定理,切线的定义,切线长定理的应用,主要考察学生的记忆能力.

练习册系列答案
相关题目
 22、定义:弦切角:顶点在圆上,一边与圆相交,另一边和圆相切的角叫弦切角.
22、定义:弦切角:顶点在圆上,一边与圆相交,另一边和圆相切的角叫弦切角.
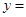 ,自变量的取值范围是
;
,自变量的取值范围是
; 定义:弦切角:顶点在圆上,一边与圆相交,另一边和圆相切的角叫弦切角.
定义:弦切角:顶点在圆上,一边与圆相交,另一边和圆相切的角叫弦切角.