摘要:解:AB=4.BC=
网址:http://m.1010jiajiao.com/timu3_id_450182[举报]
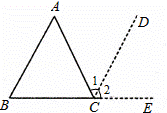
21、解:因为∠B=∠C
所以AB∥CD(
又因为AB∥EF
所以EF∥CD(
所以∠BGF=∠C(
(2)如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3
试说明:AD平分∠BAC
解:因为AD⊥BC,EG⊥BC
所以AD∥EG(
所以∠1=∠E(
∠2=∠3(
又因为∠3=∠E
所以∠1=∠2
所以AD平分∠BAC(
(3)如图,EF∥AD,∠1=∠2,∠BAC=70°.求∠AGD的度数.
解:因为EF∥AD,
所以∠2=
又因为∠1=∠2
所以∠1=∠3 (
所以AB∥
所以∠BAC+
因为∠BAC=70°
所以∠AGD=
查看习题详情和答案>>

所以AB∥CD(
内错角相等,两直线平行
)又因为AB∥EF
所以EF∥CD(
平行线的传递性
)所以∠BGF=∠C(
两直线平行,同位角相等
)(2)如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3

试说明:AD平分∠BAC
解:因为AD⊥BC,EG⊥BC
所以AD∥EG(
同垂直于一条直线的两个垂线段平行
)所以∠1=∠E(
两直线平行,同位角相等
)∠2=∠3(
两直线平行,内错角相等
)又因为∠3=∠E
所以∠1=∠2
所以AD平分∠BAC(
等量代换
)(3)如图,EF∥AD,∠1=∠2,∠BAC=70°.求∠AGD的度数.
解:因为EF∥AD,

所以∠2=
3
(
两直线平行,同位角相等
)又因为∠1=∠2
所以∠1=∠3 (
等量代换
)所以AB∥
DG
(
内错角相等,两直线平行
)所以∠BAC+
∠DGA
=180°(
两直线平行,同旁内角互补
)因为∠BAC=70°
所以∠AGD=
110°
解:因为∠B=∠C
所以AB∥CD(________)
又因为AB∥EF
所以EF∥CD(________)
所以∠BGF=∠C(________)
(2)如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3
试说明:AD平分∠BAC
解:因为AD⊥BC,EG⊥BC
所以AD∥EG(________)
所以∠1=∠E(________)
∠2=∠3(________ )
又因为∠3=∠E
所以∠1=∠2
所以AD平分∠BAC(________)
(3)如图,EF∥AD,∠1=∠2,∠BAC=70°.求∠AGD的度数.
解:因为EF∥AD,
所以∠2=________ (________)
又因为∠1=∠2
所以∠1=∠3 (________)
所以AB∥________ (________)
所以∠BAC+________=180°(________)
因为∠BAC=70°
所以∠AGD=________.
查看习题详情和答案>>
解:∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∠1=∠A(已作)
∴AB∥CD ( )
∴∠B= ∠2 ( )
而∠ACB+∠1+∠2=180°
∴∠ACB+ ∠B + ∠A =180°( )
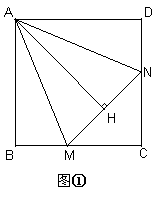
解:(1)如图①AH=AB
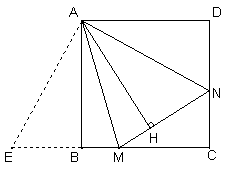
 (2)数量关系成立.如图②,延长CB至E,使BE=DN
(2)数量关系成立.如图②,延长CB至E,使BE=DN
∵ABCD是正方形
∴AB=AD,∠D=∠ABE=90°
∴Rt△AEB≌Rt△AND
∴AE=AN,∠EAB=∠NAD
∴∠EAM=∠NAM=45°
∵AM=AM
∴△AEM≌△ANM
∵AB、AH是△AEM和△ANM对应边上的高,
 ∴AB=AH
∴AB=AH
(3)如图③分别沿AM、AN翻折△AMH和△ANH,
得到△ABM和△AND
∴BM=2,DN=3,∠B=∠D=∠BAD=90°
分别延长BM和DN交于点C,得正方形ABCE.
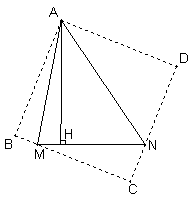 由(2)可知,AH=AB=BC=CD=AD.
由(2)可知,AH=AB=BC=CD=AD.
设AH=x,则MC=![]() , NC=
, NC=![]() 图②
图②
在Rt⊿MCN中,由勾股定理,得
![]()
∴![]()
解得![]() .(不符合题意,舍去)
.(不符合题意,舍去)
∴AH=6.
查看习题详情和答案>>