摘要:填空题: ①一个外角等于它的一个内角的正多边形是正 边形. ②正八边形的中心角的度数为 ,每一个内角度数为 ,每一个外角度数为 . ③边长为6cm的正三角形的半径是 cm,边心距是 cm,面积是 cm. ④面积等于cm2的正六边形的周长是 . ⑤同圆的内接正三角形与外切正三角形的边长之比是 . ⑥正多边形的面积是240cm2,周长是60cm2,则边心距是 cm. ⑦正六边形的两对边之间的距离是12cm,则边长是 cm. ⑧同圆的外切正四边形与内接正四边形的边心距之比是 . ⑨同圆的内接正三角形的边心距与正六边形的边心距之比是 .
网址:http://m.1010jiajiao.com/timu3_id_450024[举报]
 25、填写下列解题过程中的推理根据:
25、填写下列解题过程中的推理根据:如图,在△ABC中,∠A=40°,∠ABC的平分线BD交AC于点D,∠BDC=70°,求∠C的度数.
对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式)
解:∵∠BDC=∠A+∠ABD
(
三角形的一个外角等于与它不相邻的两个内角的和
)∵∠A=40°,∠BDC=70°(已知)
∴∠ABD=
30
°(等式的性质)∵BD平分∠ABC(已知)
∴∠ABC=2∠ABD(
角平分线的定义
)∴∠ABC=60°(等式的性质)
∵∠A+∠ABC+∠C=
180
°(三角形的内角和是180°)∠A=40°(已知),∠ABC=60°(已求)
∴∠C=
80
°(等式的性质) 24、如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E在CB的延长线上,∠ACD=55°.
24、如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E在CB的延长线上,∠ACD=55°.(1)直接写出∠BCD度数;
(2)求∠ABE的度数.
对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).
解:(1)∠BCD=
35
度(2)∵CD⊥AB(
已知
),∴∠CDB=
90
度.∵∠ABE=∠CDB+∠BCD(
三角形的一个外角等于与它不相邻的两个内角的和
),∴∠ABE=
90°
+35°
=125
度(等量代换).
情境一
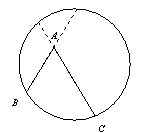
我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角.
我们还知道:①圆心角的度数等于与它所对的弧的度数,②同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.由此,小明得到一个正确的结论:圆周角的度数等于它所对的弧的度数的一半.如图1,∠LMN=
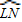 .
.
问题1 填空:如图1,如果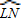 的度数是80,那么∠LMN的度数是______.
的度数是80,那么∠LMN的度数是______.
情境二
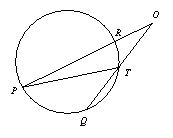
小明把顶点在圆外,并且两边都和圆相交的角叫圆外角,并继续探索.
如图2,∵∠PTQ是△OPT的一个外角,
∴∠PTQ=∠O+∠P.
∴∠O=∠PTQ-∠P.
∵圆周角的度数等于它所对的弧的度数的一半(已在情境一中证明),
∴∠PTQ=
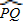 ,∠P=
,∠P=
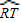 .
.
∴∠O=∠PTQ-∠P=
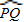 -
-
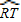 =
= (
(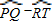 ).
).
经历了上述探索、证明过程,小明发现了“圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半”这个正确结论.
问题2 填空:如图2,如果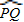 =80°,
=80°,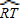 =20°,那么∠O=______°.
=20°,那么∠O=______°.
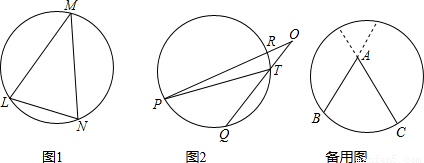
问题3 类比情境二的内容,请你就角的顶点在圆内的情况进行探索.写出你的发现,并证明你的结论.
查看习题详情和答案>>
我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角.
我们还知道:①圆心角的度数等于与它所对的弧的度数,②同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.由此,小明得到一个正确的结论:圆周角的度数等于它所对的弧的度数的一半.如图1,∠LMN=

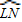 .
.问题1 填空:如图1,如果
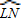 的度数是80,那么∠LMN的度数是______.
的度数是80,那么∠LMN的度数是______.情境二
小明把顶点在圆外,并且两边都和圆相交的角叫圆外角,并继续探索.
如图2,∵∠PTQ是△OPT的一个外角,
∴∠PTQ=∠O+∠P.
∴∠O=∠PTQ-∠P.
∵圆周角的度数等于它所对的弧的度数的一半(已在情境一中证明),
∴∠PTQ=

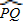 ,∠P=
,∠P=
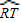 .
.∴∠O=∠PTQ-∠P=

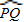 -
-
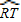 =
= (
(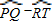 ).
).经历了上述探索、证明过程,小明发现了“圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半”这个正确结论.
问题2 填空:如图2,如果
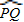 =80°,
=80°,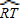 =20°,那么∠O=______°.
=20°,那么∠O=______°.问题3 类比情境二的内容,请你就角的顶点在圆内的情况进行探索.写出你的发现,并证明你的结论.

查看习题详情和答案>>
情境一
我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角.
我们还知道:①圆心角的度数等于与它所对的弧的度数,②同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.由此,小明得到一个正确的结论:圆周角的度数等于它所对的弧的度数的一半.如图1,∠LMN=
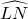 .
.
问题1 填空:如图1,如果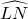 的度数是80,那么∠LMN的度数是________.
的度数是80,那么∠LMN的度数是________.
情境二
小明把顶点在圆外,并且两边都和圆相交的角叫圆外角,并继续探索.
如图2,∵∠PTQ是△OPT的一个外角,
∴∠PTQ=∠O+∠P.
∴∠O=∠PTQ-∠P.
∵圆周角的度数等于它所对的弧的度数的一半(已在情境一中证明),
∴∠PTQ=
 ,∠P=
,∠P=
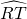 .
.
∴∠O=∠PTQ-∠P=
 -
-
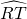 =
= (
(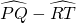 ).
).
经历了上述探索、证明过程,小明发现了“圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半”这个正确结论.
问题2 填空:如图2,如果 =80°,
=80°,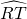 =20°,那么∠O=________°.
=20°,那么∠O=________°.
问题3 类比情境二的内容,请你就角的顶点在圆内的情况进行探索.写出你的发现,并证明你的结论.
查看习题详情和答案>>
情境一
我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角.我们还知道:①圆心角的度数等于与它所对的弧的度数,②同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.由此,小明得到一个正确的结论:圆周角的度数等于它所对的弧的度数的一半.如图1,∠LMN=![]()
![]() .
.
问题1 填空:如图1,如果![]() 的度数是80,那么∠LMN的度数是______.
的度数是80,那么∠LMN的度数是______.
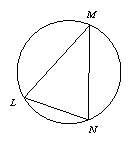 图
图
1
情境二
小明把顶点在圆外,并且两边都和圆相交的角叫圆外角,并继续探索.
如图2,∵∠PTQ是△OPT的一个外角,
∴∠PTQ=∠O+∠P.
∴∠O=∠PTQ -∠P.
∵圆周角的度数等于它所对的弧的度数的一半(已在情境一中
证明),
∴∠PTQ=![]()
![]() ,∠P=
,∠P=![]()
![]() .
.
∴∠O=∠PTQ -∠P=![]()
![]() -
-![]()
![]() =
=![]() (
(![]() -
-![]() ).
).
经历了上述探索、证明过程,小明发现了“圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半”这个正确结论.
问题2 填空:如图2,如果![]() =80°,
=80°,![]() =20°,那么∠O=______°.
=20°,那么∠O=______°.
问题3 类比情境二的内容,请你就角的顶点在圆内的情况进行探索.写出你的发现,并证明你的结论.