题目内容
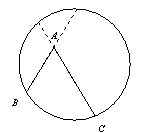
情境一我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角.
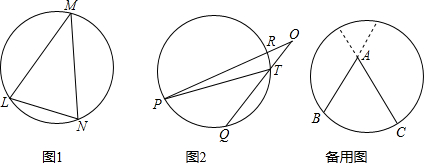
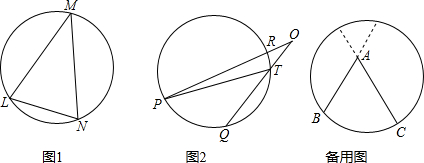
我们还知道:①圆心角的度数等于与它所对的弧的度数,②同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.由此,小明得到一个正确的结论:圆周角的度数等于它所对的弧的度数的一半.如图1,∠LMN=

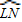 .
.问题1 填空:如图1,如果
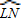 的度数是80,那么∠LMN的度数是______.
的度数是80,那么∠LMN的度数是______.情境二
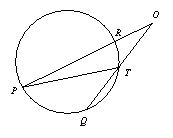
小明把顶点在圆外,并且两边都和圆相交的角叫圆外角,并继续探索.
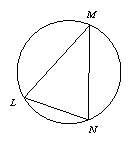
如图2,∵∠PTQ是△OPT的一个外角,
∴∠PTQ=∠O+∠P.
∴∠O=∠PTQ-∠P.
∵圆周角的度数等于它所对的弧的度数的一半(已在情境一中证明),
∴∠PTQ=

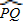 ,∠P=
,∠P=
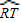 .
.∴∠O=∠PTQ-∠P=

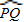 -
-
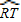 =
= (
(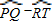 ).
).经历了上述探索、证明过程,小明发现了“圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半”这个正确结论.
问题2 填空:如图2,如果
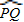 =80°,
=80°, =20°,那么∠O=______°.
=20°,那么∠O=______°.问题3 类比情境二的内容,请你就角的顶点在圆内的情况进行探索.写出你的发现,并证明你的结论.
【答案】分析:问题1:根据圆心角定理得出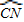 所对圆心角度数,再利用圆周角定理得出答案即可.
所对圆心角度数,再利用圆周角定理得出答案即可.
问题2:利用证明的结论圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半,得出∠O的度数即可.
问题3:利用图形可以得出圆内角的度数等于它和它的对顶角所对两弧的度数和的一半,根据圆周角定理得出∠C=
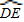 ,∠D=
,∠D=
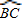 ,再利用三角形的外角性质得出答案即可.
,再利用三角形的外角性质得出答案即可.
解答:解:
 问题1:
问题1:
∵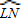 的度数是80,
的度数是80,
∴ 所对圆心角为80°,
所对圆心角为80°,
∴∠LMN的度数是: ×80=40,
×80=40,
故答案为:40.
问题2:∵圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半,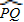 =80°,
=80°,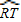 =20°
=20°
∴∠O= (80°-20°)=30°.
(80°-20°)=30°.
故答案为:30;
问题3:顶点在圆内的角叫圆内角.(圆内角的名称可以用其他名称替代),
圆内角的度数等于它和它的对顶角所对两弧的度数和的一半.
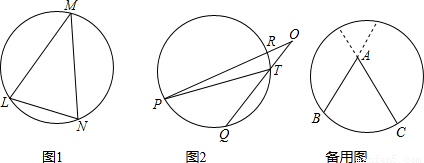
证明:如图,延长BA,交圆于点D,延长CA,交圆于点E,连接CD.
∵∠BAC是△ACD 的一个外角,
∴∠BAC=∠C+∠D.
∵圆周角的度数等于它所对的弧的度数的一半(已在情境一中证明),
∴∠C=
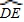 ,∠D=
,∠D=
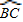 .
.
∴∠BAC=∠C+∠D=
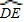 +
+
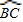 =
= (
(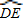 +
+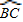 ).
).
∴命题成立.
点评:此题主要考查了圆周角定理的应用以及弧度与圆心角的关系和探索性问题,根据已知探索方法进行模仿变式进而得出新的规律是解题关键.
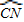 所对圆心角度数,再利用圆周角定理得出答案即可.
所对圆心角度数,再利用圆周角定理得出答案即可.问题2:利用证明的结论圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半,得出∠O的度数即可.
问题3:利用图形可以得出圆内角的度数等于它和它的对顶角所对两弧的度数和的一半,根据圆周角定理得出∠C=

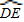 ,∠D=
,∠D=
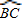 ,再利用三角形的外角性质得出答案即可.
,再利用三角形的外角性质得出答案即可.解答:解:
 问题1:
问题1:∵
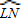 的度数是80,
的度数是80,∴
 所对圆心角为80°,
所对圆心角为80°,∴∠LMN的度数是:
 ×80=40,
×80=40,故答案为:40.
问题2:∵圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半,
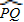 =80°,
=80°,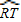 =20°
=20°∴∠O=
 (80°-20°)=30°.
(80°-20°)=30°.故答案为:30;
问题3:顶点在圆内的角叫圆内角.(圆内角的名称可以用其他名称替代),
圆内角的度数等于它和它的对顶角所对两弧的度数和的一半.
证明:如图,延长BA,交圆于点D,延长CA,交圆于点E,连接CD.
∵∠BAC是△ACD 的一个外角,
∴∠BAC=∠C+∠D.
∵圆周角的度数等于它所对的弧的度数的一半(已在情境一中证明),
∴∠C=

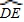 ,∠D=
,∠D=
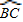 .
.∴∠BAC=∠C+∠D=

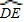 +
+
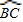 =
= (
(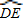 +
+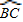 ).
).∴命题成立.
点评:此题主要考查了圆周角定理的应用以及弧度与圆心角的关系和探索性问题,根据已知探索方法进行模仿变式进而得出新的规律是解题关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目


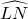 .
. ,∠P=
,∠P=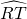 .
. ).
).
 图
图