摘要： 抛物线y=ax2+bx+c 交x轴于点A.B(1.0).交y轴于点C.顶点为P.以PA为直径的⊙D恰好过点C. (1)求点P.C.D的坐标 , (2)求抛物线的解析式, (3)抛物线上是否存在一点Q.使△QPA为直角三角形? 若存在,求出点Q的坐标,若不存在,请说明理由. 解:
网址：http://m.1010jiajiao.com/timu3_id_448158[举报]
抛物线y＝ax2＋bx＋c(a＜0)交x轴于点A(－1，0)、B(3，0)，交y轴于点C，顶点为D，以BD为直径的⊙M恰好过点C．
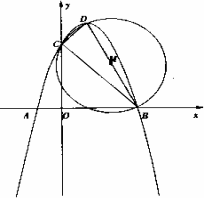
(1)求顶点D的坐标(用a的代数式表示)；
(2)求抛物线的解析式；
(3)抛物线上是否存在点P使△PBD为直角三角形？若存在，求出点P的坐标；若不存在，说明理由．
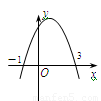
如图，抛物线y＝ax2＋bx＋c交x轴于（－1，0）、（3，0）两点，则下列判断中，错误的是（ ）
| A．图象的对称轴是直线x＝1 |
| B．当x＞1时，y随x的增大而减小 |
| C．一元二次方程ax2＋bx＋c＝0的两个根是－1和3 |
| D．当－1＜x＜3时，y＜0 |
如图，抛物线y＝ax2＋bx＋c与x轴交于点A(x1，0)、B(x2，0)(x1＜0＜x2)，与y轴交于点C(0，－2)．若OB＝4OA，且以AB为直径的圆过C点，求此抛物线的函数关系式．
如图，抛物线y＝ax2＋bx＋c交x轴于(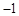
，0)、(3，0)两点，则下列判断中，错误的是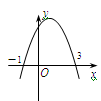
| A．图象的对称轴是直线x＝1 |
| B．当x＞1时，y随x的增大而减小 |
| C．一元二次方程ax2＋bx＋c＝0的两个根是－1和3 |
| D．当－1＜x＜3时，y＜0 |
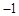，0)、(3，0)两点，则下列判断中，错误的是