Question

抛物线y＝ax²＋bx＋c(a＜0)交x轴于点A(－1，0)、B(3，0)，交y轴于点C，顶点为D，以BD为直径的⊙M恰好过点C．

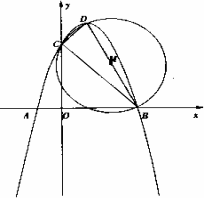
(1)求顶点D的坐标(用a的代数式表示)；

(2)求抛物线的解析式；

(3)抛物线上是否存在点P使△PBD为直角三角形？若存在，求出点P的坐标；若不存在，说明理由．

Answer 1

答案：
解析：

(1)由题意：设抛物线的解析式为y＝a(x＋1)(x－3)， 　　∴y＝ax2－2ax－3a＝a(x－1)2－4a． 　　∴点C(O，－3a)，D(1，－4a)． 　　(2)过点D作DE⊥y轴于点E，易证△DEC∽△COB． 　　∴，∴．∴a2＝l，∵a＜0，∴a＝－1． 　　故抛物线的解析式为：y＝－x2＋2x＋3． 　　(3)符合条件的点P存在，共3个． 　　①若∠BPD＝90°，P点与C点重合，则Pl(0，3)(P1表示第一个P点，下同)②若∠DBP＝90°，过点P2作P2R⊥x轴于点R，设⊙M交x轴于另一点H，设点P2(p，－p2＋2p＋3)， 　　由△BP2R∽△DBH得，＝，即， 　　解得p＝－或p＝3(舍去)．故p2(－，－)． 　　③若∠BDP＝90°，设DP3的延长线交y轴于点N，过点D作DE⊥y轴于点E可证△NDE∽△HDB， 　　求得EN＝，∴N(O，)，求得DN的解析式为y＝x＋． 　　求抛物线与直线DN的交点得P3(，)， 　　综上所述：符合条件的点P为(0，3)、(－，－)、(，)．