题目内容
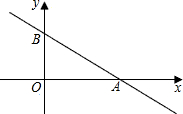 如图:直线y=kx+3与x轴、y轴分别交于A、B两点,
如图:直线y=kx+3与x轴、y轴分别交于A、B两点,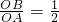 ,点C(x,y)是直线y=kx+3上与A、B不重合的动点.
,点C(x,y)是直线y=kx+3上与A、B不重合的动点.
(1)求直线y=kx+3的解析式;
(2)当点C运动到什么位置时△AOC的面积是6;
(3)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB全等?若存在,请求出点C的坐标;若不存在,请说明理由.
解:(1)令x=0,则y=3,
∴点B(0,3),OB=3,
∵ =
= ,
,
∴OA=2OB=2×3=6,
∴点A(6,0),
把点A代入直线y=kx+3得,6k+3=0,
解得k=- ,
,
∴直线解析式为y=- x+3;
x+3;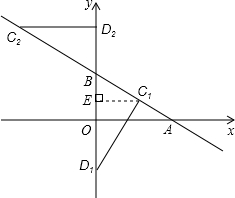
(2)设点C到x轴的距离为h,
由题意得, ×6h=6,
×6h=6,
解得h=2,
∴点C的纵坐标为2或-2,
∴- x+3=2或-
x+3=2或- x+3=-2,
x+3=-2,
解得x=2或x=10,
∴点C的坐标为(2,2)或(10,2);
(3)由勾股定理得,AB= =
=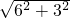 =3
=3 ,
,
①BC和BO是对应边时,∵△BCD与△AOB全等,
∴BC=BO=3,
过点C作CE⊥y轴于E,则CE∥OA,
∴∠BCE=∠BAO,
∴BE=BC•sin∠BCE=3× =
= ,
,
∴点C的纵坐标为3- ,
,
代入直线y=- x+3得,-
x+3得,- x+3=3-
x+3=3- ,
,
解得x= ,
,
此时,点C的坐标为C1( ,3-
,3- );
);
②BD和BO是对应边时,∵△BCD与△AOB全等,
∴BD=BO=3,
∴OD=3+3=6,
∴点C的纵坐标为6,
代入直线y=- x+3得,-
x+3得,- x+3=6,
x+3=6,
解得x=-6,
此时,点C的坐标C2(-6,6),
综上所述,点C( ,3-
,3- )或(-6,6)时,△BCD与△AOB全等.
)或(-6,6)时,△BCD与△AOB全等.
分析:(1)令x=0求出点B的坐标,从而得到OB的长度,再求出OA的长,然后得到点A的坐标,再代入直线解析式计算即可得解;
(2)设点C到x轴的距离为h,根据三角形的面积求出h,然后分两种情况表示出点C的纵坐标,再代入直线解析式计算求出横坐标,然后写出点C的坐标即可;
(3)利用勾股定理列式求出AB,然后分①BC和BO是对应边时,根据全等三角形对应边相等求出BC,过点C作CE⊥y轴于E,利用∠BCE的正弦求出BE的长,再求出点C的纵坐标,然后代入直线解析式求解得到点C的横坐标,从而得解;②BD和BO是对应边时,根据全等三角形对应边相等求出BD,再求出OD,即为点C的纵坐标,然后代入直线解析式求解得到点C的横坐标,从而得解.
点评:本题是一次函数综合题型,主要利用了一次函数与坐标轴交点的求解,待定系数法求一次函数解析式,三角形的面积,一次函数图象上点的坐标特征,全等三角形对应边相等的性质,(2)难点在于点C的纵坐标有正数和负数两种情况,(3)难点在于OB的对应边有BC和BD两种情况.
∴点B(0,3),OB=3,
∵
 =
= ,
,∴OA=2OB=2×3=6,
∴点A(6,0),
把点A代入直线y=kx+3得,6k+3=0,
解得k=-
 ,
,∴直线解析式为y=-
 x+3;
x+3;
(2)设点C到x轴的距离为h,
由题意得,
 ×6h=6,
×6h=6,解得h=2,
∴点C的纵坐标为2或-2,
∴-
 x+3=2或-
x+3=2或- x+3=-2,
x+3=-2,解得x=2或x=10,
∴点C的坐标为(2,2)或(10,2);
(3)由勾股定理得,AB=
 =
=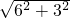 =3
=3 ,
,①BC和BO是对应边时,∵△BCD与△AOB全等,
∴BC=BO=3,
过点C作CE⊥y轴于E,则CE∥OA,
∴∠BCE=∠BAO,
∴BE=BC•sin∠BCE=3×
 =
= ,
,∴点C的纵坐标为3-
 ,
,代入直线y=-
 x+3得,-
x+3得,- x+3=3-
x+3=3- ,
,解得x=
 ,
,此时,点C的坐标为C1(
 ,3-
,3- );
);②BD和BO是对应边时,∵△BCD与△AOB全等,
∴BD=BO=3,
∴OD=3+3=6,
∴点C的纵坐标为6,
代入直线y=-
 x+3得,-
x+3得,- x+3=6,
x+3=6,解得x=-6,
此时,点C的坐标C2(-6,6),
综上所述,点C(
 ,3-
,3- )或(-6,6)时,△BCD与△AOB全等.
)或(-6,6)时,△BCD与△AOB全等.分析:(1)令x=0求出点B的坐标,从而得到OB的长度,再求出OA的长,然后得到点A的坐标,再代入直线解析式计算即可得解;
(2)设点C到x轴的距离为h,根据三角形的面积求出h,然后分两种情况表示出点C的纵坐标,再代入直线解析式计算求出横坐标,然后写出点C的坐标即可;
(3)利用勾股定理列式求出AB,然后分①BC和BO是对应边时,根据全等三角形对应边相等求出BC,过点C作CE⊥y轴于E,利用∠BCE的正弦求出BE的长,再求出点C的纵坐标,然后代入直线解析式求解得到点C的横坐标,从而得解;②BD和BO是对应边时,根据全等三角形对应边相等求出BD,再求出OD,即为点C的纵坐标,然后代入直线解析式求解得到点C的横坐标,从而得解.
点评:本题是一次函数综合题型,主要利用了一次函数与坐标轴交点的求解,待定系数法求一次函数解析式,三角形的面积,一次函数图象上点的坐标特征,全等三角形对应边相等的性质,(2)难点在于点C的纵坐标有正数和负数两种情况,(3)难点在于OB的对应边有BC和BD两种情况.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
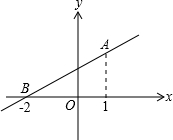 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为