题目内容
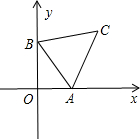
 如图:直线y=-
如图:直线y=-
| ||
| 3 |
| 3 |
分析:因为点P是动点,所以从特殊位置(相切)入手分析,分右相切和左相切两种情况,然后求解.
解答:解:若圆和直线相切,则圆心到直线的距离应等于圆的半径1,
据直线的解析式求得A(3,0),B(0,
),
则tan∠BAO=
=
,
所以∠BAO=30°,
所以当相切时,AP=2,
点P可能在点A的左侧或右侧.所以要相交,应介于这两种情况之间,则3-2<m<3+2,即1<m<5.
故选B.
据直线的解析式求得A(3,0),B(0,
| 3 |
则tan∠BAO=
| BO |
| AO |
| ||
| 3 |
所以∠BAO=30°,
所以当相切时,AP=2,
点P可能在点A的左侧或右侧.所以要相交,应介于这两种情况之间,则3-2<m<3+2,即1<m<5.
故选B.
点评:此题主要考查了直线与坐标轴的求法,以及三角函数的运用,题目综合性较强,注意特殊点的求法是解决问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 如图,直线y=-
如图,直线y=- 9、如图,直线AB、CD相交于O,∠COE是直角,∠1=57°,则∠2=
9、如图,直线AB、CD相交于O,∠COE是直角,∠1=57°,则∠2= 如图,直线AB的解析式为y=
如图,直线AB的解析式为y= 如图,直线y=x+2与双曲线
如图,直线y=x+2与双曲线 如图,直线AB,CD分别交直线EF于点G,H,AB∥CD,则图中与∠AGE相等的角有
如图,直线AB,CD分别交直线EF于点G,H,AB∥CD,则图中与∠AGE相等的角有