题目内容
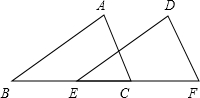 已知:如图,同一直线上有四点B、E、C、F,且 AB∥DE,AC∥DF,BE=CF.
已知:如图,同一直线上有四点B、E、C、F,且 AB∥DE,AC∥DF,BE=CF.求证:AB=DE.
分析:根据线段间的距离求得BE+EC=CF+BC,即BC=EF,然后由两直线AB∥DE,AC∥DF,推知同位角∠B=∠DEF,∠ACB=∠F,所以根据全等三角形的判定定理ASA证明△ABC≌△DEF;最后由全等三角形的对应边相等证明结论即可.
解答:证明:∵BE=CF(已知),
∴BE+EC=CF+BC,即BC=EF;
又∵AB∥DE,AC∥DF,
∴∠B=∠DEF(两直线平行,同位角相等),
∠ACB=∠F(两直线平行,同位角相等);
∴在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AB=DE(全等三角形的对应边相等).
∴BE+EC=CF+BC,即BC=EF;
又∵AB∥DE,AC∥DF,
∴∠B=∠DEF(两直线平行,同位角相等),
∠ACB=∠F(两直线平行,同位角相等);
∴在△ABC和△DEF中,
|
∴△ABC≌△DEF(ASA),
∴AB=DE(全等三角形的对应边相等).
点评:本题考查了全等三角形的判定与性质.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
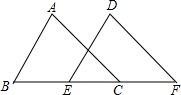 已知:如图,同一直线上有四点B、E、C、F,且∠A=∠D,∠B=∠DEF,BE=CF.
已知:如图,同一直线上有四点B、E、C、F,且∠A=∠D,∠B=∠DEF,BE=CF.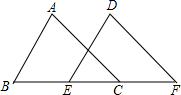 已知:如图,同一直线上有四点B、E、C、F,且∠A=∠D,∠B=∠DEF,BE=CF.
已知:如图,同一直线上有四点B、E、C、F,且∠A=∠D,∠B=∠DEF,BE=CF.
