题目内容
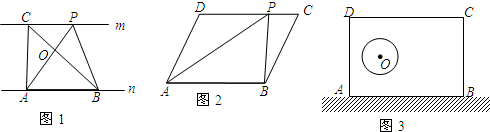
探究规律:已知,如图1,直线m∥n,A、B为直线n上的两点,C、P为直线m上的两点.若A、B、C为三个定点,P为动点,则
(1)△PAB与△CAB的面积大小关系为
(2)请你在图1中再画出一个与△ABC面积相等的△DEF,并说明面积相等的理由.
解决问题:
问题1:如图2,在?ABCD中,点P是CD上任意一点,
则S△PAB
问题2:如图3,在公路旁边,有一块矩形的土地ABCD,其内部有一个底面为圆形的建筑物,点O为圆心.若要将土地(不含圆形建筑物所占的面积)平均分给两家承包,且分割线都过公路边(AB)上一点P,请你确定点P的位置,并画出分割线,说明理由.
分析:(1)根据同底等高的两个三角形面积相等,得出结论;
(2)根据平行四边形(矩形)的对边相等的性质,结合(1)的结论,得以对边为底边的两个三角形面积和,等于以对边为底边的一个三角形的面积.
(2)根据平行四边形(矩形)的对边相等的性质,结合(1)的结论,得以对边为底边的两个三角形面积和,等于以对边为底边的一个三角形的面积.
解答:解:探究规律:
(1)S△PAB=S△CAB;
(2)如图1,在直线n上取EF=AB,在直线m上任取一点D,则S△ABC=S△DEF;
理由:等底等高的两个三角形面积相等;
解决问题:
(1)答案为:=;
(2)连接DO并延长,交AB于点P,连接PC,则折线DP-PC为所求分割线,如图3所示.
理由:∵S△PCD=S△ADP+S△BCP,
∴S△PCD-
S⊙O=S△ADP+S△BCP-
S⊙O,
即△PCD内所含土地的面积与△ADP和△BCP内所含土地的面积相等.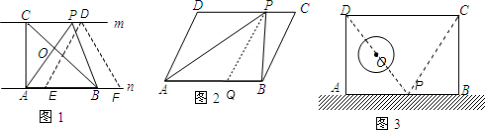
(1)S△PAB=S△CAB;
(2)如图1,在直线n上取EF=AB,在直线m上任取一点D,则S△ABC=S△DEF;
理由:等底等高的两个三角形面积相等;
解决问题:
(1)答案为:=;
(2)连接DO并延长,交AB于点P,连接PC,则折线DP-PC为所求分割线,如图3所示.
理由:∵S△PCD=S△ADP+S△BCP,
∴S△PCD-
| 1 |
| 2 |
| 1 |
| 2 |
即△PCD内所含土地的面积与△ADP和△BCP内所含土地的面积相等.

点评:本题考查了作图的应用与设计.关键是根据等底等高的两个三角形面积相等的性质,解决实际问题.

练习册系列答案
相关题目