摘要:4.如图13.△ABC中.AB=AC.∠A=45°.AC的垂直平分线分别交AB.AC于D.E两点.连接CD.如果AD=1.那么tan∠BCD= .
网址:http://m.1010jiajiao.com/timu3_id_447483[举报]
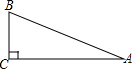 如图,在△ABC中,∠C=90゜,AC=12,AB=13,则sinA=
如图,在△ABC中,∠C=90゜,AC=12,AB=13,则sinA=| 5 |
| 13 |
| 5 |
| 13 |
| 12 |
| 13 |
| 12 |
| 13 |
| 5 |
| 12 |
| 5 |
| 12 |
| 12 |
| 13 |
| 12 |
| 13 |
| 5 |
| 13 |
| 5 |
| 13 |
| 12 |
| 5 |
| 12 |
| 5 |
在△ABC中,AB、BC、AC三边的长分别为
、
、
,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
(1)△ABC的面积为:
(2)若△DEF三边的长分别为
、
、
,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为
(3)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.
(4)如图4,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13m2、25m2、36m2,则六边形花坛ABCDEF的面积是

查看习题详情和答案>>
| 5 |
| 10 |
| 13 |
(1)△ABC的面积为:
3.5
3.5
.(2)若△DEF三边的长分别为
| 5 |
| 8 |
| 17 |
3
3
.(3)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.
(4)如图4,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13m2、25m2、36m2,则六边形花坛ABCDEF的面积是
110
110
m2.
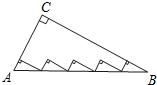 10、如图:直角△ABC中,AC=5,BC=12,AB=13,则内部五个小直角三角形的周长为
10、如图:直角△ABC中,AC=5,BC=12,AB=13,则内部五个小直角三角形的周长为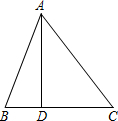 已知:如图,在△ABC中,D为边BC上的一点,AB=13,AD=12,AC=15,BD=5.求△ABC的面积.
已知:如图,在△ABC中,D为边BC上的一点,AB=13,AD=12,AC=15,BD=5.求△ABC的面积. (2012•普陀区二模)已知:如图,在△ABC中,CD⊥AB,sinA=
(2012•普陀区二模)已知:如图,在△ABC中,CD⊥AB,sinA=