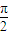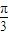摘要：3．设M={平面内的点(a,b)}.N={f(x)|f(x)=acos2x+bsin2x} .给出M到N的映射: f:(a,b)f(x)= acos2x+bsin2x.则点(1,)的象f(x)的最小正周期为: A．π B．2π C． D．
网址：http://m.1010jiajiao.com/timu3_id_4473242[举报]
设M={ 平面内的点（m，n）}，N={f（x）|f（x）=mcos2x+nsin2x}，给出M到N的映射f：（m，n）→f（x）=mcos2x+nsin2x，则点(2，
)的像f（x）的最小正周期是（ ）
| 3 |
| A、π | ||
B、
| ||
| C、2π | ||
D、
|
设M={ 平面内的点（m，n）}，N={f（x）|f（x）=mcos2x+nsin2x}，给出M到N的映射f：（m，n）→f（x）=mcos2x+nsin2x，则点(2，
)的像f（x）的最小正周期是（ ）
查看习题详情和答案>>
| 3 |
| A．π | B．
| C．2π | D．
|
设M={ 平面内的点（m，n）}，N={f（x）|f（x）=mcos2x+nsin2x}，给出M到N的映射f：（m，n）→f（x）=mcos2x+nsin2x，则点
的像f（x）的最小正周期是（ ）
A．π
B．
C．2π
D．
查看习题详情和答案>>
的像f（x）的最小正周期是（ ）A．π
B．
C．2π
D．
查看习题详情和答案>>
的像f（x）的最小正周期是（ ）
的像f（x）的最小正周期是（ ）
