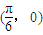题目内容
设M={ 平面内的点(m,n)},N={f(x)|f(x)=mcos2x+nsin2x},给出M到N的映射f:(m,n)→f(x)=mcos2x+nsin2x,则点 的像f(x)的最小正周期是( )
的像f(x)的最小正周期是( )A.π
B.

C.2π
D.

【答案】分析:通过题目定义,求出像f(x)的表达式,利用三角函数的有关公式化简表达式为:一个角的三角函数的形式,然后求出它的周期即可.
解答:解:设M={ 平面内的点(m,n)},N={f(x)|f(x)=mcos2x+nsin2x},给出M到N的映射f:(m,n)→f(x)=mcos2x+nsin2x,
点 的像f(x)=2cos2x+
的像f(x)=2cos2x+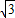 sin2x=cos2x+
sin2x=cos2x+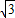 sin2x+1=2sin(2x+
sin2x+1=2sin(2x+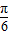 )+1
)+1
所以函数的最小正周期是: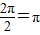
故选A
点评:本题是基础题,考查三角函数的最小正周期的求法,二倍角公式、两角和的正弦函数的应用,考查计算能力.
解答:解:设M={ 平面内的点(m,n)},N={f(x)|f(x)=mcos2x+nsin2x},给出M到N的映射f:(m,n)→f(x)=mcos2x+nsin2x,
点
 的像f(x)=2cos2x+
的像f(x)=2cos2x+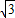 sin2x=cos2x+
sin2x=cos2x+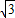 sin2x+1=2sin(2x+
sin2x+1=2sin(2x+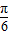 )+1
)+1所以函数的最小正周期是:
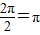
故选A
点评:本题是基础题,考查三角函数的最小正周期的求法,二倍角公式、两角和的正弦函数的应用,考查计算能力.

练习册系列答案
相关题目
 的像f(x)的图象可以由曲线y=2sin2x按向量
的像f(x)的图象可以由曲线y=2sin2x按向量 平移得到,则向量
平移得到,则向量 的坐标为( )
的坐标为( )



 的像f(x)的图象可以由曲线y=2sin2x按向量
的像f(x)的图象可以由曲线y=2sin2x按向量 平移得到,则向量
平移得到,则向量 的坐标为( )
的坐标为( )