摘要：7． 已知f(x)=.则的值为 A.-1 B.--2 C.-2 D.-3
网址：http://m.1010jiajiao.com/timu3_id_4472522[举报]
已知f(x)＝
及g(x)＝
．
(1)求f(x)、g(x)的定义域及f(x)·g(x)的值；
(2)求f(x)的最小值；
(3)若a＝
，b＝t
，c＝x＋1，是否存在满足下列条件的正数t，使得对于任意的正数x，a、b、c都可以成为某个三角形三边的长？若存在，则求出t的取值范围；若不存在，请说明理由．
已知f（x）=a2x-
x3，x∈（-2，2）为正常数．
（1）可以证明：定理“若a、b∈R*，则
≥
（当且仅当a=b时取等号）”推广到三个正数时结论是正确的，试写出推广后的结论（无需证明）；
（2）若f（x）＞0在（0，2）上恒成立，且函数f（x）的最大值大于1，求实数a的取值范围，并由此猜测y=f（x）的单调性（无需证明）；
（3）对满足（2）的条件的一个常数a，设x=x1时，f（x）取得最大值．试构造一个定义在D={x|x＞-2，且x≠4k-2，k∈N}上的函数g（x），使当x∈（-2，2）时，g（x）=f（x），当x∈D时，g（x）取得最大值的自变量的值构成以x1为首项的等差数列． 查看习题详情和答案>>
| 1 |
| 2 |
（1）可以证明：定理“若a、b∈R*，则
| a+b |
| 2 |
| ab |
（2）若f（x）＞0在（0，2）上恒成立，且函数f（x）的最大值大于1，求实数a的取值范围，并由此猜测y=f（x）的单调性（无需证明）；
（3）对满足（2）的条件的一个常数a，设x=x1时，f（x）取得最大值．试构造一个定义在D={x|x＞-2，且x≠4k-2，k∈N}上的函数g（x），使当x∈（-2，2）时，g（x）=f（x），当x∈D时，g（x）取得最大值的自变量的值构成以x1为首项的等差数列． 查看习题详情和答案>>
已知f（x）是定义在R上的且以2为周期的偶函数，当0≤x≤1时，f（x）=x2，如果直线y=x+a与曲线y=f（x）恰有两个不同的交点，则实数a的值为（ ）
| A、2k（k∈Z） | ||
B、2k或2k+
| ||
| C、0 | ||
D、2k或2k-
|
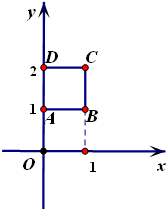已知f（x）=2|x-1|，该函数在区间[a，b]上的值域为[1，2]，记满足该条件的实数a、b所形成的实数对为点P（a，b），则由点P构成的点集组成的图形为（ ）