题目内容
已知f(x)是定义在R上的且以2为周期的偶函数,当0≤x≤1时,f(x)=x2,如果直线y=x+a与曲线y=f(x)恰有两个不同的交点,则实数a的值为( )
| A、2k(k∈Z) | ||
B、2k或2k+
| ||
| C、0 | ||
D、2k或2k-
|
分析:先求出-1≤x≤0时f(x)的解析式,即得x∈[-1,1]时f(x)的解析式,再据周期性可得 x∈[2k-1,2k+1]时f(x)的解析式,如图,直线y=x+a的斜率为1,在y轴上的截距等于a,故直线过顶点或与曲线相切时,满足条件.
解答: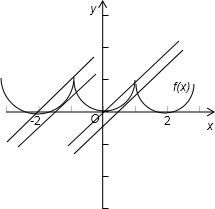 解:设-1≤x≤0,则 0≤-x≤1,f(-x)=(-x)2=x2=f(x),
解:设-1≤x≤0,则 0≤-x≤1,f(-x)=(-x)2=x2=f(x),
综上,f(x)=x2,x∈[-1,1],f(x)=(x-2k)2,x∈[2k-1,2k+1],
由于直线y=x+a的斜率为1,在y轴上的截距等于a,在一个周期[-1,1]上,
a=0时 满足条件,a=-
时,在此周期上直线和曲线相切,
并和曲线在下一个区间上图象
有一个交点,也满足条件. 由于f(x)的周期为2,
故在定义域内,满足条件的a 应是 2k+0 或 2k-
,k∈Z.
故选 D.
 解:设-1≤x≤0,则 0≤-x≤1,f(-x)=(-x)2=x2=f(x),
解:设-1≤x≤0,则 0≤-x≤1,f(-x)=(-x)2=x2=f(x),综上,f(x)=x2,x∈[-1,1],f(x)=(x-2k)2,x∈[2k-1,2k+1],
由于直线y=x+a的斜率为1,在y轴上的截距等于a,在一个周期[-1,1]上,
a=0时 满足条件,a=-
| 1 |
| 4 |
并和曲线在下一个区间上图象
有一个交点,也满足条件. 由于f(x)的周期为2,
故在定义域内,满足条件的a 应是 2k+0 或 2k-
| 1 |
| 4 |
故选 D.
点评:本题考查函数的周期性、奇偶性、求函数的解析式,体现了数形结合的数学思想.

练习册系列答案
相关题目