摘要：已知函数f(x)=-x3+ax2+b 图像上任意不同的两点连线斜率小于1.求证:-＜a＜ 若x∈［0,1］,函数y=f(x)上任一点切线斜率为k,讨论|k|≤1的充要条件 解:(1)设任意不同的两点P1(x1,y1),P2(x2,y2),且x1≠x2 则＜1 ∴＜1 即-x12-x1x2-x22+a(x1+x2)＜1 ∴-x12+(a-x2)x1-x22+ax2-1＜0 ∵x1∈R ∴Δ=(a-x2)2+4(-x22+ax2-1)＜0 即-3x22+2ax2+a2-4＜0 ∴-3(x2-)2++a2-4＜0 ∴a2-4＜0,∴-＜a＜ (2)当x∈［0,1］时.k=f′(x)=-3x2+2ax 由题意知:-1≤-3x2+2ax≤1,x∈［0,1］ 即对于任意x∈［0,1］,|f′|.|f′(1)|. |f′()|的值满足 或 或 即 或 或 ∴1≤a≤ 即|k|≤1的充要条件是1≤a≤
网址：http://m.1010jiajiao.com/timu3_id_4471580[举报]
已知函数f(x)=-x3+ax2+b(a，bÎR)。
（1）是否存在实数使函数f(x)在R上是单调函数？
（2）若xÎ[0，1]，函数y=f(x)上任意一点切线的斜率为k，讨论|k|£1的充要条件。
查看习题详情和答案>>
已知函数f(x)=-x3+ax2+b(a，bÎR)。
（1）是否存在实数使函数f(x)在R上是单调函数？
（2）若xÎ[0，1]，函数y=f(x)上任意一点切线的斜率为k，讨论|k|£1的充要条件。
查看习题详情和答案>>已知函数f(x)=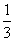
x3-ax2+bx（a，b∈R），
（Ⅰ）若f′(0)=f′(2)=1，求函数f(x)的解析式；
（Ⅱ）若b=a+2，且f(x)在区间（0，1）上单调递增，求实数a的取值范围。
查看习题详情和答案>>
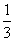x3-ax2+bx（a，b∈R），（Ⅰ）若f′(0)=f′(2)=1，求函数f(x)的解析式；
（Ⅱ）若b=a+2，且f(x)在区间（0，1）上单调递增，求实数a的取值范围。
x3+
ax2+bx+1(a、b∈R,b≥-2)在区间［-
,
］单调递减,设g(x)=-3f(x)+mx2-6x(m∈R).
恒成立,求实数m的取值范围.