题目内容
已知函数f(x)=-x3+ax2+b(a,bÎR)。
(1)是否存在实数使函数f(x)在R上是单调函数?
(2)若xÎ[0,1],函数y=f(x)上任意一点切线的斜率为k,讨论|k|£1的充要条件。
答案:
解析:
解析:
解(1)∵ f(x)=-x3+ax2+b ∴ f¢(x)=-3x2+2ax ∴ f¢(x)不可能恒大于0,若-3x2+2ax£0恒成立,则a=0,故当a=0,bÎR时函数f(x)在R上是单调减函数。 (2)当xÎ[0,1]时,k=f¢(x)=-3x2+2ax,由题意得:-1£-3x2+2ax£1,xÎ[0,1] 即对任意xÎ[0,1],|f¢(x)|£1等价于|f¢(0)|£1,|f¢(1)|£1,
或 所以 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
 或
或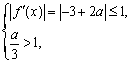
 即
即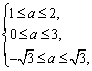 或
或