题目内容
已知函数f(x)=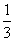 x3-ax2+bx(a,b∈R),
x3-ax2+bx(a,b∈R),
(Ⅰ)若f′(0)=f′(2)=1,求函数f(x)的解析式;
(Ⅱ)若b=a+2,且f(x)在区间(0,1)上单调递增,求实数a的取值范围。
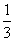 x3-ax2+bx(a,b∈R),
x3-ax2+bx(a,b∈R),(Ⅰ)若f′(0)=f′(2)=1,求函数f(x)的解析式;
(Ⅱ)若b=a+2,且f(x)在区间(0,1)上单调递增,求实数a的取值范围。
解:(Ⅰ)因为 ,
,
由 即
即 得
得 ,
,
所以f(x)的解析式为 。
。
(Ⅱ)若b=a+2,则 ,
,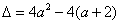 ,
,
(1)当△≤0,即-1≤a≤2时,f′(x)≥0恒成立,那么f(x)在R上单调递增,
所以,当-1≤a≤2时,f(x)在区间(0,1)上单调递增;
(2)当△>0,即a>2或a<-1时,因为 的对称轴方程为x=a,
的对称轴方程为x=a,
要使函数f(x)在区间(0,1)上单调递增,
需 或
或 ,解得-2≤a<-1或2<a≤3;
,解得-2≤a<-1或2<a≤3;
综上:当a∈[-2,3]时,函数f(x)在区间(0,1)上单调递增。
 ,
,由
 即
即 得
得 ,
,所以f(x)的解析式为
 。
。(Ⅱ)若b=a+2,则
 ,
,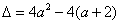 ,
,(1)当△≤0,即-1≤a≤2时,f′(x)≥0恒成立,那么f(x)在R上单调递增,
所以,当-1≤a≤2时,f(x)在区间(0,1)上单调递增;
(2)当△>0,即a>2或a<-1时,因为
 的对称轴方程为x=a,
的对称轴方程为x=a,要使函数f(x)在区间(0,1)上单调递增,
需
 或
或 ,解得-2≤a<-1或2<a≤3;
,解得-2≤a<-1或2<a≤3;综上:当a∈[-2,3]时,函数f(x)在区间(0,1)上单调递增。

练习册系列答案
相关题目