题目内容
(本题12分)已知关于 的不等式
的不等式 ,其中
,其中 .
.
(Ⅰ)当 变化时,试求不等式的解集
变化时,试求不等式的解集 ;
;
(Ⅱ)对于不等式的解集 ,若满足
,若满足 (其中
(其中 为整数集). 试探究集合
为整数集). 试探究集合 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合 中元素个数最少的
中元素个数最少的 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合 ;若不能,请说明理由.
;若不能,请说明理由.
【答案】
当 时,集合
时,集合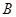 的元素个数最少.
…………………10分
的元素个数最少.
…………………10分
此时 ,故集合
,故集合
【解析】解:(Ⅰ)当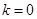 时,
时,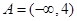 ;
…………………2分
;
…………………2分
当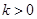 且
且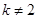 时,
时,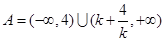 ;
;
当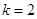 时,
时,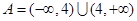 ;(不单独分析
;(不单独分析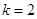 时的情况不扣分)………………4分
时的情况不扣分)………………4分
当 时,
时, .
…………………6分
.
…………………6分
(Ⅱ)由(1)知:当 时,集合
时,集合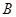 中的元素的个数无限; …………………8分
中的元素的个数无限; …………………8分
当 时,集合
时,集合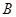 中的元素的个数有限,此时集合
中的元素的个数有限,此时集合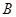 为有限集.
为有限集.
因为 ,当且仅当
,当且仅当 时取等号,
时取等号,
所以当 时,集合
时,集合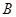 的元素个数最少.
…………………10分
的元素个数最少.
…………………10分
此时 ,故集合
,故集合 .
…………………12分
.
…………………12分

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 道备选题中一次性抽取
道备选题中一次性抽取 道题独立作答,然后由乙回答剩余
道题独立作答,然后由乙回答剩余 题就停止答题,即闯关成功.已知在
题就停止答题,即闯关成功.已知在 道题,乙答对每道题的概率都是
道题,乙答对每道题的概率都是 .
.