题目内容
(本题12分)已知函数 .
.
(1)当 时,求函数
时,求函数 的单调递减区间;
的单调递减区间;
(2)当 时,
时, 在
在 上恒大于0,求实数
上恒大于0,求实数 的取值范围.
的取值范围.
【答案】
(1) 
(2) 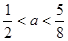
【解析】解:(1) ,
,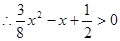 ,得
,得 ,
,
函数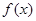 在区间
在区间 上递减. ……………………………………………4分
上递减. ……………………………………………4分
(2)由题意得, 对任意的
对任意的 恒成立 ………………1分
恒成立 ………………1分
法一: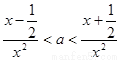 ,对任意的
,对任意的 恒成立
恒成立
所以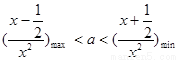 ,
, ………………………………2分
………………………………2分
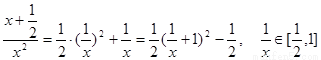 ,所以
,所以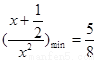 …2分
…2分
同理 …………………………………………………………2分
…………………………………………………………2分
所以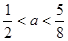 ………………………………………………………………1分
………………………………………………………………1分
法二: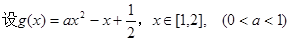
 ………………………………………………1分
………………………………………………1分
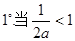 ,即
,即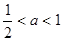 时,
时,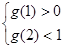 ,解得
,解得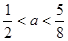 .
.
 ,即
,即 时,
时, ,无解.
,无解.
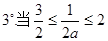 ,即
,即 时,
时, ,无解.
,无解.
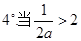 ,即
,即 时,
时, ,无解. ……………………6分
,无解. ……………………6分
综上: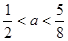 . …………………………………………………………1分
. …………………………………………………………1分
法三:由题意得, 对任意的
对任意的 恒成立 ……………1分
恒成立 ……………1分
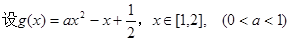 ,
,
则 ,解得
,解得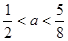 . ………………………………………3分
. ………………………………………3分
再验证:当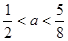 时,
时,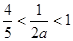 ,
,
所以, ,
, ,
,
故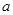 的取值范围为
的取值范围为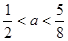 . …………………………………………………4分
. …………………………………………………4分

练习册系列答案
相关题目
 有极值,且曲线
有极值,且曲线 处的切线斜率为3.
处的切线斜率为3. 的解析式;
的解析式; 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。 有三个零点,求实数
有三个零点,求实数 的取值范围.
的取值范围.