题目内容
(本题12分)已知函数 的图像关于原点对称,并且当
的图像关于原点对称,并且当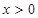 时,
时, ,试求
,试求 在
在 上的表达式,并画出它的图像,根据图像写出它的单调区间。
上的表达式,并画出它的图像,根据图像写出它的单调区间。
【答案】
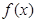 的单调递增区间为
的单调递增区间为 和
和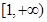 ;递减区间为
;递减区间为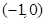 和
和 .
.
【解析】本试题主要是考察了函数的图像以及函数的单调性,奇偶性的运用。
可以利用奇偶性求解函数的解析式,然后作出函数图像,根据图像求解函数的单调区间。
解: 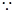
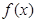 的图像关于原点对称,
的图像关于原点对称,
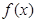 是奇函数,
是奇函数, .
.
又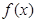 在
在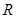 上
上
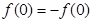 ,解得
,解得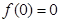 .
.
若 ,则
,则 ,
,




于是有 .……8分
.……8分
函数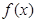 的图像如图所示:…………………10分
的图像如图所示:…………………10分
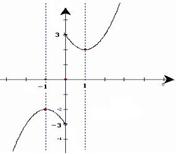
由图像可知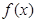 的单调递增区间为
的单调递增区间为 和
和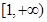 ;
;
递减区间为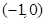 和
和 .……………………12分
.……………………12分

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 有极值,且曲线
有极值,且曲线 处的切线斜率为3.
处的切线斜率为3. 的解析式;
的解析式; 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。 有三个零点,求实数
有三个零点,求实数 的取值范围.
的取值范围.