摘要：已知抛物线M的方程为 (1)求抛物线M的准线的方程, (2)求证:对任意.经过两点的直线与一定圆C想切.并求出圆C的方程, (3)设AB为定圆C的任意一条被直线平分的弦.求证:所有这些弦所在的直线都与某一条抛物线有且仅有一个公共点. (1)解:抛物线M的准线的方程为.即. (2)证明:∵. ∴经过两点的直线方程为, ∵原点到这条直线的距离. ∴定圆C的方程为. (3)证明:设AB与直线的交点为.则.AB的方程为. 由题意设抛物线方程为.把代入AB的方程.得 .由.得. 即所有这些弦所在的直线都与抛物线有且仅有一个公共点.
网址：http://m.1010jiajiao.com/timu3_id_4471037[举报]
已知抛物线C的方程为x2=4y，直线y=2与抛物线C相交于M，N两点，点A，B在抛物线C上．（Ⅰ）若∠BMN=∠AMN，求证：直线AB的斜率为定值；
（Ⅱ）若直线AB的斜率为
| 2 |
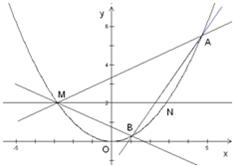已知抛物线C的方程为x2=4y，直线y=2与抛物线C相交于M，N两点，点A，B在抛物线C上．（Ⅰ）若∠BMN=∠AMN，求证：直线AB的斜率为
| 2 |
（Ⅱ）若直线AB的斜率为
| 2 |
已知抛物线C的方程为y2=2x，焦点为F，
（1）若C的准线与x轴的交点为D，过D的直线l与C交于A，B两点，且|
|=2|
|，求直线l的斜率；
（2）设点P是C上的动点，点R，N在y轴上，圆M：（x-1）2+y2=1内切于△PRN，求△PRN面积的最小值．
查看习题详情和答案>>
（1）若C的准线与x轴的交点为D，过D的直线l与C交于A，B两点，且|
. |
| FA |
. |
| FB |
（2）设点P是C上的动点，点R，N在y轴上，圆M：（x-1）2+y2=1内切于△PRN，求△PRN面积的最小值．