题目内容
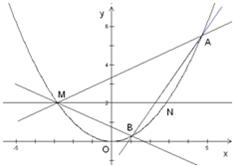 已知抛物线C的方程为x2=4y,直线y=2与抛物线C相交于M,N两点,点A,B在抛物线C上.
已知抛物线C的方程为x2=4y,直线y=2与抛物线C相交于M,N两点,点A,B在抛物线C上.(Ⅰ)若∠BMN=∠AMN,求证:直线AB的斜率为
| 2 |
(Ⅱ)若直线AB的斜率为
| 2 |
分析:(Ⅰ)设A(x1,y1),B(x2,y2),直线AM的斜率为k,由∠BMN=∠AMN,所以直线BM的斜率为-k,可求得M(-2
,2),N(2
,2),则直线AM的方程为y=k(x+2
)-2,由此能够证明直线AB的斜率为
.
(Ⅱ)若直线AB的斜率为
,由x1=4kAM+2
,x2=4kBM+2
,得
kAB=
=
=
=
=
,由此能求出点N到直线MA,MB的距离相等.
| 2 |
| 2 |
| 2 |
| 2 |
(Ⅱ)若直线AB的斜率为
| 2 |
| 2 |
| 2 |
kAB=
| y1-y2 |
| x1-x2 |
| ||||||||
| x1-x2 |
| x1+x2 |
| 4 |
4(kAM+kBM)+4
| ||
| 4 |
| 2 |
解答:解:(Ⅰ)设A(x1,y1),B(x2,y2),直线AM的斜率为k,∵∠BMN=∠AMN,所以直线BM的斜率为-k,
可求得M(-2
,2),N(2
,2),则直线AM的方程为y=k(x+2
)-2,
代入x2=4y得x2-4kx-8
k-8=0,∵xAx1=-8
k-8∴x1=4k+2
,
同理x2=-4k+2
,kAB=
=
=
=
.(5分)
(Ⅱ)若直线AB的斜率为
,由(1)可得:x1=4kAM+2
,x2=4kBM+2
,
∴kAB=
=
=
=
=
,
∴kAM+kBM=0,
∴∠BMN=∠AMN,
故点N到直线MA,MB的距离相等.(10分)
可求得M(-2
| 2 |
| 2 |
| 2 |
代入x2=4y得x2-4kx-8
| 2 |
| 2 |
| 2 |
同理x2=-4k+2
| 2 |
| y1-y2 |
| x1-x2 |
| ||||||||
| x1-x2 |
| x1+x2 |
| 4 |
| 2 |
(Ⅱ)若直线AB的斜率为
| 2 |
| 2 |
| 2 |
∴kAB=
| y1-y2 |
| x1-x2 |
| ||||||||
| x1-x2 |
| x1+x2 |
| 4 |
4(kAM+kBM)+4
| ||
| 4 |
| 2 |
∴kAM+kBM=0,
∴∠BMN=∠AMN,
故点N到直线MA,MB的距离相等.(10分)
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
 (2011•合肥三模)已知抛物线C的方程为x2=2py(p>0),过抛物线上点M(-2
(2011•合肥三模)已知抛物线C的方程为x2=2py(p>0),过抛物线上点M(-2 已知抛物线C的方程为x2=2py(p>0),焦点F为 (0,1),点P(x1,y1)是抛物线上的任意一点,过点P作抛物线的切线交抛物线的准线l于点A(s,t).
已知抛物线C的方程为x2=2py(p>0),焦点F为 (0,1),点P(x1,y1)是抛物线上的任意一点,过点P作抛物线的切线交抛物线的准线l于点A(s,t).