题目内容
已知抛物线C1的方程为y=x2,抛物线C2的方程为y=2-x2,C1和C2交于A,B两点,D是曲线段AOB段上异于A,B的任意一点,直线AD交C2于点E,G为△BDE的重心,过G作C1的两条切线,切点分别为M,N,求线段MN的长度的取值范围.
分析:设切点N(x1,x12),M(x2,x22),由题设条件推导出3x12-6x1+4x0-1=0,3x22-6x2+4x0-1=0,由此能求出线段MN的长度的取值范围.
解答:解:设A(-1,1),B(1,1),D(x0,x02),(-1<x0<1),…(2分)
直线AD:y=(x0-1)x+x0,代入y=2-x2,
E(2-x0,-x02+4x0-2),D(1,
),
设切点N(x1,x12),M(x2,x22),
2x1=
,3x12-6x1+4x0-1=0,
同理,3x22-6x2+4x0-1=0,
则x1,x2是方程3x2-6x+4x0-1=0的两根,…(6分)
∴|NM|=
=
,(-1<x0<1)…(10分)
则|MN|∈(0,
).…(12分)
直线AD:y=(x0-1)x+x0,代入y=2-x2,
E(2-x0,-x02+4x0-2),D(1,
| 4x0-1 |
| 3 |
设切点N(x1,x12),M(x2,x22),
2x1=
| ||
| 1-x1 |
同理,3x22-6x2+4x0-1=0,
则x1,x2是方程3x2-6x+4x0-1=0的两根,…(6分)
∴|NM|=
| (x12-x12)2+(x1-x2)2 |
4
| ||
| 3 |
| 1-x0 |
则|MN|∈(0,
4
| ||
| 3 |
点评:本题考查线段长度的取值范围的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
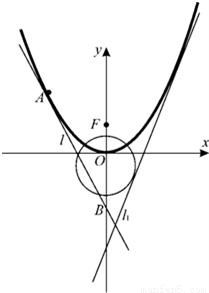
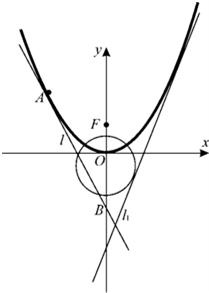 已知抛物线C1的方程为y=ax2(a>0),圆C2的方程为x2+(y+1)2=5,直线l1:y=2x+m(m<0)是C1、C2的公切线.F是C1的焦点.
已知抛物线C1的方程为y=ax2(a>0),圆C2的方程为x2+(y+1)2=5,直线l1:y=2x+m(m<0)是C1、C2的公切线.F是C1的焦点.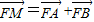 ,证明:点M在一定直线上.
,证明:点M在一定直线上.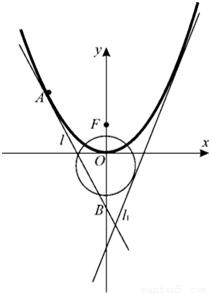
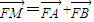 ,证明:点M在一定直线上.
,证明:点M在一定直线上.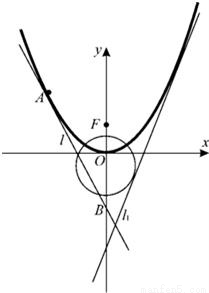
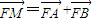 ,证明:点M在一定直线上.
,证明:点M在一定直线上.