摘要:(13)在下图中.直线L为曲线C在点P处的切线.则直线L的斜率是 (14)如图.直角三角形ABC中..△ABD为等腰直角三角形..当点D到平面ABC距离最大时.直线CD与平面ABC所成角为 (15)平面内满足不等式组(x+y-4)(x+ 2y-6)≤0.x≥0.y≥0的所有点中.使目标函数z=5x+4y取得最大值的点的坐标是 (16)已知O为原点.点P (x.y)在单位圆x2 + y2 = 1上.点Q (2cosθ, 2sinθ)满足 =().则 = .三.解答题:本大题6个小题.共74分.解答必需写出必要的文字说明.推理过程或计算步骤. (17) 解不等式 (18) 某公交公司对某线路客源情况统计显示.公交车从每个停靠点出发后.乘客人数及频率如下表: 人数 0~6 7~12 13~18 19~24 25~30 31人以上 频率 0.1 0.15 0.25 0.20 0.20 0.1 (I)从每个停靠点出发后.乘客人数不超过24人的概率约是多少? (II)全线途经10个停靠点.若有2个以上.乘客人数超过18人的概率大于0.9.公交公司就要考虑在该线路增加一个班次.请问该线路需要增加班次吗? (19) 在三棱柱中.底面为正三角形... (I)求证:, (II)把四棱锥绕直线旋转到.使平面与平面重合.试求旋转过的角的余弦值. (20) 已知锐角α.β满足2sinβ=sin(2α+β)且α+β≠. (I)求证:tan(α+β)=3tanα (II)设y=tanβ, x=tanα, α∈[.]试求函数y=f (x)的最大值 (21) 设Sn为数列{an}的前n项和.如果Sn=2an-3n+5. (I)证明:数列{an+3}是等比数列, (II)是否存在正整数p.q.r(p<q<r)使得p,q, r和Sp.Sq.Sr同时成等差数列?若存在.求出p.q.r的值.若不存在.请说明理由. 椭圆的左焦点为F.过F作垂直于x轴的直线与椭圆交于点M.N.相应的准线与x轴交于点H.求证:∠MHN为锐角,且直线MH与椭圆有且仅有一个公共点. (Ⅱ)请针对抛物线y=.类比(I).写出一个真命题. (Ⅲ)动直线l与(Ⅱ)中抛物线交于不同的两点A.B.满足=m(m∈R),抛物线在点A处的切线为l1.在点B处切线l2.切线l1与l2交点为T.求证:点T在准线上. 绝密★启用前 宿迁市2004-2005学年度高三年级第三次考试
网址:http://m.1010jiajiao.com/timu3_id_4470673[举报]
.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
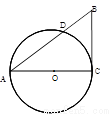
A.(几何证明选讲选做题)如图,已知 的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=
;
的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=
;
B.(不等式选讲选做题)关于x的不等式 的解集为空集,则实数a的取值范围是
;
的解集为空集,则实数a的取值范围是
;
C.(坐标系与参数方程选做题)已知极坐标的极点在直角坐标系的原点O处,极轴与x轴的正半轴重合,曲线C的参数方程为 (
( 为参数),直线l的极坐标方程为
为参数),直线l的极坐标方程为 .点P在曲线C上,则点P到直线l的距离的最小值为
.
.点P在曲线C上,则点P到直线l的距离的最小值为
.
查看习题详情和答案>>
如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足 ,
, .
.
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过定点F(1,0)作互相垂直的直线l与l',l与(1)中的轨迹C交于A、B两点,l'与(1)中的轨迹C交于D、E两点,求四边形ADBE面积S的最小值;
(3)(在下列两题中,任选一题,写出计算过程,并求出结果,若同时选做两题,
则只批阅第②小题,第①题的解答,不管正确与否,一律视为无效,不予批阅):
①将(1)中的曲线C推广为椭圆: ,并
,并
将(2)中的定点取为焦点F(1,0),求与(2)相类似的问题的解;
②(解答本题,最多得9分)将(1)中的曲线C推广为椭圆: ,并
,并
将(2)中的定点取为原点,求与(2)相类似的问题的解.
 查看习题详情和答案>>
查看习题详情和答案>>
 ,
, .
.(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过定点F(1,0)作互相垂直的直线l与l',l与(1)中的轨迹C交于A、B两点,l'与(1)中的轨迹C交于D、E两点,求四边形ADBE面积S的最小值;
(3)(在下列两题中,任选一题,写出计算过程,并求出结果,若同时选做两题,
则只批阅第②小题,第①题的解答,不管正确与否,一律视为无效,不予批阅):
①将(1)中的曲线C推广为椭圆:
 ,并
,并将(2)中的定点取为焦点F(1,0),求与(2)相类似的问题的解;
②(解答本题,最多得9分)将(1)中的曲线C推广为椭圆:
 ,并
,并将(2)中的定点取为原点,求与(2)相类似的问题的解.
 查看习题详情和答案>>
查看习题详情和答案>>
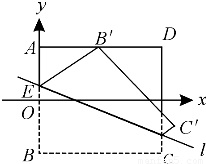
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕,正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B′;折痕l与AB交于点E,点M满足关系式 =
=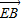 +
+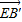 .
.
(1)如图,建立以AB中点为原点的直角坐标系,求点M的轨迹方程;
(2)若曲线C是由点M的轨迹及其关于边AB对称的曲线组成的,
F是AB边上的一点,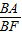 =4,过点F的直线交曲线C于P、Q两点,且
=4,过点F的直线交曲线C于P、Q两点,且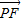 =λ
=λ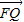 ,求实数λ的取值范围.
,求实数λ的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>
 =
=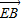 +
+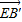 .
.(1)如图,建立以AB中点为原点的直角坐标系,求点M的轨迹方程;
(2)若曲线C是由点M的轨迹及其关于边AB对称的曲线组成的,
F是AB边上的一点,
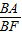 =4,过点F的直线交曲线C于P、Q两点,且
=4,过点F的直线交曲线C于P、Q两点,且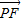 =λ
=λ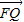 ,求实数λ的取值范围.
,求实数λ的取值范围. 查看习题详情和答案>>
查看习题详情和答案>>
 (a>0,b>0)过点P(
(a>0,b>0)过点P( ),上、下焦点分别为F1、F2,向量
),上、下焦点分别为F1、F2,向量 .直线l与椭圆交于A,B两点,线段AB中点为m(
.直线l与椭圆交于A,B两点,线段AB中点为m( ).
).