摘要: 设n为不小于2的正整数.记n的所有正约数,已知P(n)=n12.则n的最小值为
网址:http://m.1010jiajiao.com/timu3_id_4470342[举报]
设n是正整数,r为正有理数.
(Ⅰ)求函数f(x)=(1+x)r+1-(r+1)x-1(x>-1)的最小值;
(Ⅱ)证明:
<nr<
;
(Ⅲ)设x∈R,记[x]为不小于x的最小整数,例如[2]=2,[π]=4,[-
]=-1.令S=
+
+
+…+
,求[S]的值.
(参考数据:80
≈344.7,81
≈350.5,124
≈618.3,126
≈631.7).
查看习题详情和答案>>
(Ⅰ)求函数f(x)=(1+x)r+1-(r+1)x-1(x>-1)的最小值;
(Ⅱ)证明:
| nr+1-(n-1)r+1 |
| r+1 |
| (n+1)r+1-nr+1 |
| r+1 |
(Ⅲ)设x∈R,记[x]为不小于x的最小整数,例如[2]=2,[π]=4,[-
| 3 |
| 2 |
| 3 | 81 |
| 3 | 82 |
| 3 | 83 |
| 3 | 125 |
(参考数据:80
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
设n是正整数,r为正有理数.
(Ⅰ)求函数f(x)=(1+x)r+1-(r+1)x-1(x>-1)的最小值;
(Ⅱ)证明:![]() ;
;
(Ⅲ)设x∈R,记[x]为不小于x的最小整数,例如[2]=2,[π]=4,[-![]() ]=-1.令S=
]=-1.令S=![]() +
+![]() +
+![]() +…+
+…+![]() ,求[S]的值.
,求[S]的值.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
(2013•湖北)设n是正整数,r为正有理数.
(Ⅰ)求函数f(x)=(1+x)r+1-(r+1)x-1(x>-1)的最小值;
(Ⅱ)证明:
<nr<
;
(Ⅲ)设x∈R,记[x]为不小于x的最小整数,例如[2]=2,[π]=4,[-
]=-1.令S=
+
+
+…+
,求[S]的值.
(参考数据:80
≈344.7,81
≈350.5,124
≈618.3,126
≈631.7).
查看习题详情和答案>>
(Ⅰ)求函数f(x)=(1+x)r+1-(r+1)x-1(x>-1)的最小值;
(Ⅱ)证明:
| nr+1-(n-1)r+1 |
| r+1 |
| (n+1)r+1-nr+1 |
| r+1 |
(Ⅲ)设x∈R,记[x]为不小于x的最小整数,例如[2]=2,[π]=4,[-
| 3 |
| 2 |
| 3 | 81 |
| 3 | 82 |
| 3 | 83 |
| 3 | 125 |
(参考数据:80
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
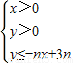 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)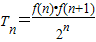 ,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;
,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;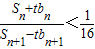 成立?若存在,求出正整数n,t;若不存在,说明理由.
成立?若存在,求出正整数n,t;若不存在,说明理由.