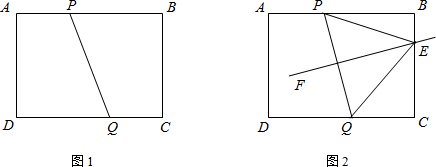
如图1.在矩形AB CD中.AB=20㎝.BC=4㎝.点P从A开始沿折线A-B-C-D以4㎝/s的速度移动.点Q从C开始沿CD边以1㎝/s的速度移动.如果点P.Q分别从A.C同时出发.当其中一点到达D——青夏教育精英家教网——

摘要：如图1.在矩形AB CD中.AB=20㎝.BC=4㎝.点P从A开始沿折线A-B-C-D以4㎝/s的速度移动.点Q从C开始沿CD边以1㎝/s的速度移动.如果点P.Q分别从A.C同时出发.当其中一点到达D时.另一点也随之停止运动.设运动时间为t(s). (1)t为何值时.四边形APQD为矩形? (2)如图2.如果⊙P和⊙Q的半径都是2㎝.那么t为何值时.⊙P和⊙Q外切?

网址：http://m.1010jiajiao.com/timu3_id_446987[举报]

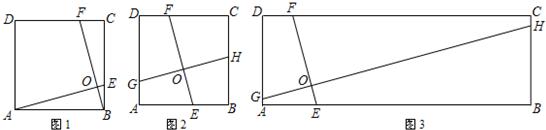
在探究矩形的性质时，小明得到了一个有趣的结论：矩形两条对角线的平方和等于四条边的平方和．如图1，在矩形ABCD中，由勾股定理，得AC²=AB²+BC²，BD²=AB²+AD²，又CD=AB，AD=BC，所以AC²+BD²=AB²+BC²+CD²+AD²=2（AB²+BC²）．
小亮对菱形进行了探究，也得到了同样的结论，于是小亮猜想：任意平行四边形两条对角线的平方和等于四条边的平方和．请你解决下列问题：
（1）如图2，已知：四边形ABCD是菱形，求证：AC²+BD²=2（AB²+BC²）；
（2）你认为小亮的猜想是否成立，如果成立，请利用图3给出证明；如果不成立，请举反例说明；
（3）如图4，在△ABC中，BC、AC、AB的长分别为a、b、c，AD是BC边上的中线．试求AD的长．（结果用a，b，c表示）

查看习题详情和答案>>

（2013•雨花台区一模）我们曾经历过探索梯形中位线性质的过程，在得到梯形中位线性质的同时也积累了许多活动经验．请利用这些经验试着解决以下问题：

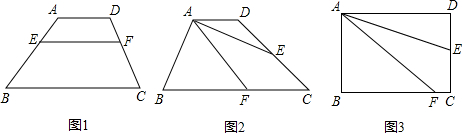
问题一、如图1，在梯形ABCD中，AD∥BC，AE=

DC，若AD=4，BC=12，则EF=

．
问题二、如图2，在梯形ABCD中，AD∥BC，F为BC边上一点，AE平分∠DAF，且点E为DC的中点，若AF=BF=6.5cm，AB=5cm，求梯形ABCD的面积．
问题三、如图3，在矩形ABCD中，F为BC边上一点，AE平分∠DAF，且点E为DC的中点，若AD=a，FC=b．请用含有a，b的代数式表示CD的长．

查看习题详情和答案>>

已知：如图①，②，在矩形ABCD中，AB=4，BC=8，P，Q分别是边BC，CD上的点．
（1）如图①，若AP⊥PQ，BP=2，求CQ的长；
（2）如图②，若

=2，且E，F，G分别为AP，PQ，PC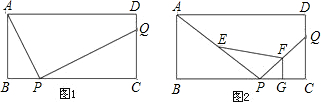

的中点，求四边形EPGF的面积．查看习题详情和答案>>

（2012•溧水县二模）如图1，在矩形ABCD中，AB=8，AD=6，点P、Q分别是AB边和CD边上的动点，点P从点A向点B运动，点Q从点C向点D运动，且保持AP=CQ．设AP=x．
（1）当PQ∥AD时，x的值等于

；
（2）如图2，线段PQ的垂直平分线EF与BC边相交于点E，连接EP、EQ，设BE=y，求y关于x的函数关系式；
（3）在问题（2）中，设△EPQ的面积为S，求S关于x的函数关系式，并求当x取何值时，S的值最小，最小值是多少？

查看习题详情和答案>>

27、（1）如图1，在正方形ABCD中，点E，F分别在边BC、CD上，AE，BF交于点O，∠AOF=90°．求证：AE=BF．
（2）如图2，在正方形ABCD中，点E、H、F、G分别在边AB、BC、CD、DA上，EF、GH交于点O，∠FOH=90°，EF=4．求GH的长．
（3）如图3，在矩形ABCD中，AB=3AD，点E、H、F、G分别在矩形ABCD的边AB、BC、CD、DA上，EF、GH交于点O，∠FOH=90°，EF=4，求GH的长．

查看习题详情和答案>>