题目内容
(2013•雨花台区一模)我们曾经历过探索梯形中位线性质的过程,在得到梯形中位线性质的同时也积累了许多活动经验.请利用这些经验试着解决以下问题:
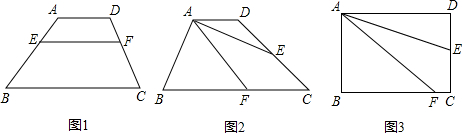
问题一、如图1,在梯形ABCD中,AD∥BC,AE=
AB,DF=
DC,若AD=4,BC=12,则EF=
.
问题二、如图2,在梯形ABCD中,AD∥BC,F为BC边上一点,AE平分∠DAF,且点E为DC的中点,若AF=BF=6.5cm,AB=5cm,求梯形ABCD的面积.
问题三、如图3,在矩形ABCD中,F为BC边上一点,AE平分∠DAF,且点E为DC的中点,若AD=a,FC=b.请用含有a,b的代数式表示CD的长.

问题一、如图1,在梯形ABCD中,AD∥BC,AE=
| 1 |
| 3 |
| 1 |
| 3 |
| 20 |
| 3 |
| 20 |
| 3 |
问题二、如图2,在梯形ABCD中,AD∥BC,F为BC边上一点,AE平分∠DAF,且点E为DC的中点,若AF=BF=6.5cm,AB=5cm,求梯形ABCD的面积.
问题三、如图3,在矩形ABCD中,F为BC边上一点,AE平分∠DAF,且点E为DC的中点,若AD=a,FC=b.请用含有a,b的代数式表示CD的长.
分析:问题一:连接AC,利用相似三角形的判定与性质得出ME,FM的长得出答案即可;
问题二:利用中位线的性质得出梯形的中位线长,进而求出△ABF的高,即可得出答案;
问题三:根据平行线分线段成比例定理的性质以及等角对等边得出AF的长,进而利用勾股定理得出AB的长,即可得出CD的长.
问题二:利用中位线的性质得出梯形的中位线长,进而求出△ABF的高,即可得出答案;
问题三:根据平行线分线段成比例定理的性质以及等角对等边得出AF的长,进而利用勾股定理得出AB的长,即可得出CD的长.
解答: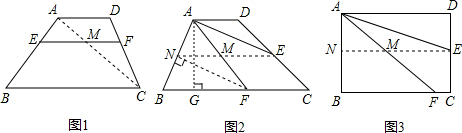 解:问题一、如图1,连接AC,
解:问题一、如图1,连接AC,
∵在梯形ABCD中,AD∥BC,AE=
AB,DF=
DC,
AD=4,BC=12,
∴
=
,
=
,
∴
=
,
=
,
解得:ME=4,FM=
,
则EF=4+
=
;
问题二、如图2,过点F作FN⊥AB于点N,连接EN,过点A作AG⊥BF于点G,
∵AF=BF=6.5cm,FN⊥AB,
∴AN=BN,
∵点E为DC的中点,
∴NE是梯形ABCD的中位线,
∴NE∥AD∥BC,
∴∠DAE=∠AEM,
此时NM=
BF=
×6.5,AM=MF,
∵AE平分∠DAF,
∴∠DAE=∠EAF,
∴∠AEM=∠EAF,
∴AM=ME=
AF=
×6.5,
∴NE=MN+ME=6.5,
∵AN=BN=2.5,BF=6.5,
解得:FN=6,
∴AG×BF=FN×AB,
则6.5AG=6×5,
解得:AG=
,
∴梯形ABCD的面积为:AG×NE=6.5×
=30;
问题三、如图3,过点E作NE∥AD于点N交AF于点M,
∵AE平分∠DAF,
∴∠DAE=∠EAF,
∵AD∥BC,AD∥NE,
∴AD∥NE∥BC,
∴∠DAE=∠AEM,
∴∠EAM=∠AEM,
∴AM=ME,
∵点E为DC的中点,
∴M为AF中点,
∴AM=MF,
∵AD=a,FC=b,
∴ME=
=
,
∴AF=a+b,
∴BF=a-b,
∴AB2=(a+b)2-(a-b)2=4ab,
∴CD=AB=2
.
故答案为:
.
 解:问题一、如图1,连接AC,
解:问题一、如图1,连接AC,∵在梯形ABCD中,AD∥BC,AE=
| 1 |
| 3 |
| 1 |
| 3 |
AD=4,BC=12,
∴
| AE |
| AB |
| EM |
| BC |
| FC |
| CD |
| FM |
| AD |
∴
| 1 |
| 3 |
| EM |
| 12 |
| 2 |
| 3 |
| FM |
| 4 |
解得:ME=4,FM=
| 8 |
| 3 |
则EF=4+
| 8 |
| 3 |
| 20 |
| 3 |
问题二、如图2,过点F作FN⊥AB于点N,连接EN,过点A作AG⊥BF于点G,
∵AF=BF=6.5cm,FN⊥AB,
∴AN=BN,
∵点E为DC的中点,
∴NE是梯形ABCD的中位线,
∴NE∥AD∥BC,
∴∠DAE=∠AEM,
此时NM=
| 1 |
| 2 |
| 1 |
| 2 |
∵AE平分∠DAF,
∴∠DAE=∠EAF,
∴∠AEM=∠EAF,
∴AM=ME=
| 1 |
| 2 |
| 1 |
| 2 |
∴NE=MN+ME=6.5,
∵AN=BN=2.5,BF=6.5,
解得:FN=6,
∴AG×BF=FN×AB,
则6.5AG=6×5,
解得:AG=
| 60 |
| 13 |
∴梯形ABCD的面积为:AG×NE=6.5×
| 60 |
| 13 |
问题三、如图3,过点E作NE∥AD于点N交AF于点M,
∵AE平分∠DAF,
∴∠DAE=∠EAF,
∵AD∥BC,AD∥NE,
∴AD∥NE∥BC,
∴∠DAE=∠AEM,
∴∠EAM=∠AEM,
∴AM=ME,
∵点E为DC的中点,
∴M为AF中点,
∴AM=MF,
∵AD=a,FC=b,
∴ME=
| AD+FC |
| 2 |
| a+b |
| 2 |
∴AF=a+b,
∴BF=a-b,
∴AB2=(a+b)2-(a-b)2=4ab,
∴CD=AB=2
| ab |
故答案为:
| 20 |
| 3 |
点评:此题主要考查了相似三角形的判定与性质以及平行线分线段成比例定理和勾股定理等知识,熟练利用平行线分线段成比例定理是解题关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 (2013•雨花台区一模)如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则sin∠BAC的值为( )
(2013•雨花台区一模)如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则sin∠BAC的值为( ) (2013•雨花台区一模)如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
(2013•雨花台区一模)如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )