题目内容
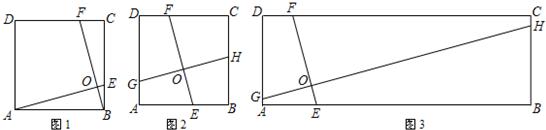
27、(1)如图1,在正方形ABCD中,点E,F分别在边BC、CD上,AE,BF交于点O,∠AOF=90°.求证:AE=BF.
(2)如图2,在正方形ABCD中,点E、H、F、G分别在边AB、BC、CD、DA上,EF、GH交于点O,∠FOH=90°,EF=4.求GH的长.
(3)如图3,在矩形ABCD中,AB=3AD,点E、H、F、G分别在矩形ABCD的边AB、BC、CD、DA上,EF、GH交于点O,∠FOH=90°,EF=4,求GH的长.
(2)如图2,在正方形ABCD中,点E、H、F、G分别在边AB、BC、CD、DA上,EF、GH交于点O,∠FOH=90°,EF=4.求GH的长.
(3)如图3,在矩形ABCD中,AB=3AD,点E、H、F、G分别在矩形ABCD的边AB、BC、CD、DA上,EF、GH交于点O,∠FOH=90°,EF=4,求GH的长.

分析:(1)根据∠AOF=90°,利用同角的余角相等得出∠EAB=∠FBC,再根据ASA即可证出△FBC≌△EAB.
(2)可以认为图2中的线段GH、FE是由图1中的线段AE、BF平移得到,故GH=FE=4.
(3)由于AB=3AD,可见图3是由三个图2的基本型转化而来,据此即可解答.
(2)可以认为图2中的线段GH、FE是由图1中的线段AE、BF平移得到,故GH=FE=4.
(3)由于AB=3AD,可见图3是由三个图2的基本型转化而来,据此即可解答.
解答:解:(1)∵∠AOF=90°,
∴∠OAB+∠FBA=90°,
又∵∠FBC+∠FBA=90°,
∴∠OAB=∠FBC.
又∵AB=BC,
∠ABE=∠BCF,
∴△ABE≌△BCF.
故AE=BF.
(2)∵图2中的线段GH、FE是由图1中的线段AE、BF平移得到,
即△ABE平移后得到△GKH,
△FBC平移后得到△FEL,
∴△GKH≌△FEL,
故GH=FE=4.
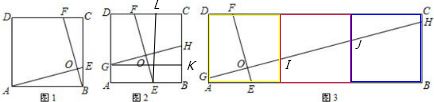
(3)把AB三等分,得到三个矩形,
将(2)过程重复,即得到GI=IJ=JH,
得GH=12.
∴∠OAB+∠FBA=90°,
又∵∠FBC+∠FBA=90°,
∴∠OAB=∠FBC.
又∵AB=BC,
∠ABE=∠BCF,
∴△ABE≌△BCF.
故AE=BF.
(2)∵图2中的线段GH、FE是由图1中的线段AE、BF平移得到,
即△ABE平移后得到△GKH,
△FBC平移后得到△FEL,
∴△GKH≌△FEL,
故GH=FE=4.
(3)把AB三等分,得到三个矩形,
将(2)过程重复,即得到GI=IJ=JH,
得GH=12.

点评:此题不仅考查了正方形的性质,还考查了平移的性质,将(2)(3)转化为(1)是解题的关键.此题体现了转化思想的重要作用.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目