摘要：画一个边长为的正方形.再以这个正方形的对角线为边画第二个正方形.以第二个正方形的对角线为边画第三个正方形.则第10个正方形的面积为 .
网址：http://m.1010jiajiao.com/timu3_id_4469749[举报]
已知首项为x1的数列{xn}满足xn+1=
（a为常数）．
（1）若对于任意的x1≠-1，有xn+2=xn对于任意的n∈N*都成立，求a的值；
（2）当a=1时，若x1＞0，数列{xn}是递增数列还是递减数列？请说明理由；
（3）当a确定后，数列{xn}由其首项x1确定，当a=2时，通过对数列{xn}的探究，写出“{xn}是有穷数列”的一个真命题（不必证明）．说明：对于第3题，将根据写出真命题所体现的思维层次和对问题探究的完整性，给予不同的评分． 查看习题详情和答案>>
| axn | xn+1 |
（1）若对于任意的x1≠-1，有xn+2=xn对于任意的n∈N*都成立，求a的值；
（2）当a=1时，若x1＞0，数列{xn}是递增数列还是递减数列？请说明理由；
（3）当a确定后，数列{xn}由其首项x1确定，当a=2时，通过对数列{xn}的探究，写出“{xn}是有穷数列”的一个真命题（不必证明）．说明：对于第3题，将根据写出真命题所体现的思维层次和对问题探究的完整性，给予不同的评分． 查看习题详情和答案>>
某次数学竞赛共3道试题，20名参赛学生的情况如下：
（1）他们每人都至少解出1题；
（2）在没有解出第1题的那些学生中，解出第2题的是解出第3题的人数的2倍；
（3）只解出第1题的比余下的学生中解出第1题的多1人;
(4)只解出1道题的学生中，有一半没有解出第1题.
试问有多少学生只解出第2题？
查看习题详情和答案>>
已知首项为x1的数列{xn}满足xn+1=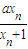
（a为常数）．
（1）若对于任意的x1≠-1，有xn+2=xn对于任意的n∈N*都成立，求a的值；
（2）当a=1时，若x1＞0，数列{xn}是递增数列还是递减数列？请说明理由；
（3）当a确定后，数列{xn}由其首项x1确定，当a=2时，通过对数列{xn}的探究，写出“{xn}是有穷数列”的一个真命题（不必证明）．说明：对于第3题，将根据写出真命题所体现的思维层次和对问题探究的完整性，给予不同的评分．
查看习题详情和答案>>
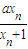（a为常数）．（1）若对于任意的x1≠-1，有xn+2=xn对于任意的n∈N*都成立，求a的值；
（2）当a=1时，若x1＞0，数列{xn}是递增数列还是递减数列？请说明理由；
（3）当a确定后，数列{xn}由其首项x1确定，当a=2时，通过对数列{xn}的探究，写出“{xn}是有穷数列”的一个真命题（不必证明）．说明：对于第3题，将根据写出真命题所体现的思维层次和对问题探究的完整性，给予不同的评分．
查看习题详情和答案>>
、
是圆锥曲线C上不与顶点重合的任意两点，
是垂直于
轴的一条垂轴弦，直线
分别交
和点
。
的代数式分别表示
和
；
（如图），求证：
是与
位置无关的定值；
，将根据研究结论所体现的思维层次，给予两种不同
层次的评分）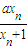 
（a为常数）．