��Ŀ����
��֪����Ϊx1������{xn}����xn+1=| axn | xn+1 |
��1�������������x1��-1����xn+2=xn���������n��N*����������a��ֵ��
��2����a=1ʱ����x1��0������{xn}�ǵ������л��ǵݼ����У���˵�����ɣ�
��3����aȷ��������{xn}��������x1ȷ������a=2ʱ��ͨ��������{xn}��̽����д����{xn}���������С���һ�������⣨����֤������˵�������ڵ�3�⣬������д�������������ֵ�˼ά��κͶ�����̽���������ԣ����費ͬ�����֣�
��������1�����xn+2������xn+1��������xn���õ�a2xn=��a+1��xn2+xn����n=1ʱ����x1�������Եõõ�a��ֵ���ɣ�
��2������Ϊ�ݼ����У���Ϊ��a=1��x1��1�õ�xn��0����xn+1-xn=
-xn=-
��0�����Ե�֤��
��3����a=2�õ�����{xn}����xn+1=
����Ϊ{xn}���������У�������x1=-
�õ����ɣ�
��2������Ϊ�ݼ����У���Ϊ��a=1��x1��1�õ�xn��0����xn+1-xn=
| xn |
| xn+1 |
| ||
| xn+1 |
��3����a=2�õ�����{xn}����xn+1=
| 2xn |
| xn+1 |
| 1 |
| 7 |
����⣺��1����xn+2=
=
=
=xn
��a2xn=��a+1��xn2+xn����n=1ʱ����x1�������Ե�
����a=-1��
��2������{xn}�ǵݼ����У�
��x1��0.xn+1=
��xn��0��n��N*��xn+1-xn=
-xn=-
��0��n��N*��
������{xn}�ǵݼ����У�
��3������������������������{xn}����xn+1=
����x1=-
����{xn}����������
| axn+1 |
| xn+1+1 |
a•
| ||
|
| a2xn |
| axn+xn+1 |
��a2xn=��a+1��xn2+xn����n=1ʱ����x1�������Ե�
|
��2������{xn}�ǵݼ����У�
��x1��0.xn+1=
| xn |
| xn+1 |
��xn��0��n��N*��xn+1-xn=
| xn |
| xn+1 |
| ||
| xn+1 |
������{xn}�ǵݼ����У�
��3������������������������{xn}����xn+1=
| 2xn |
| xn+1 |
| 1 |
| 7 |
����������ѧ�����������еĵ���ʽ�����ѧ���⣬���ж�һ�������ǵݼ���������У�

��ϰ��ϵ�д�
�����Ŀ
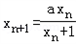 ��a��������
��a�������� ��a��������
��a��������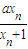 ��a��������
��a��������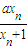 ��a��������
��a��������