摘要:已知函数的图象与轴分别相交于点A.B.(分别是与轴正半轴同方向的单位向量).函数. (1)求的值, (2)当满足时.求函数的最小值. [思路点拨]本题是以向量为背景.解析法为手段.考查解析思想的运用和处理函数性质的方法.考查运算能力和运用数学模型的能力. [正确解答] (1)由已知得A(,0),B(0,b),则={,b},于是=2,b=2. ∴k=1,b=2. ,得x+2>x2-x-6,即<0, 得-2<x<4, ==x+2+-5 由于x+2>0,则≥-3,其中等号当且仅当x+2=1,即x=-1时成立 ∴的最小值是-3. [解后反思]要熟悉在其函数的定义域内.常见模型函数求最值的常规方法.如型.
网址:http://m.1010jiajiao.com/timu3_id_4469247[举报]

 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围; 的最小值;
的最小值; 的图象C1与函数
的图象C1与函数 的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.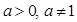 ,设
,设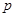 :函数
:函数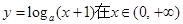 内单调递减;
内单调递减;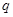 :二次函数
:二次函数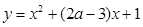 的图象与
的图象与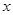 轴交于不同的两点.如果
轴交于不同的两点.如果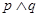 为假命题,
为假命题,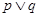 为真命题,求
为真命题,求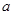 的取值范围.
的取值范围.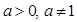 ,设
,设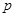 :函数
:函数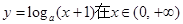 内单调递减;
内单调递减;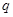 :二次函数
:二次函数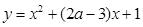 的图象与
的图象与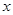 轴交于不同的两点.如果
轴交于不同的两点.如果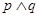 为假命题,
为假命题,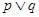 为真命题,求
为真命题,求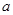 的取值范围.
的取值范围.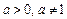 ,设P:函数
,设P:函数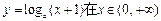 内单调递减;Q:二次函数
内单调递减;Q:二次函数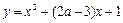 的图象与
的图象与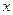 轴交于不同的两点. 如果P与Q有且只有一个正确,求
轴交于不同的两点. 如果P与Q有且只有一个正确,求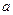 的取值范围.
的取值范围.  .
. 在
在 处取得极值为-1.求
处取得极值为-1.求 、
、 的值;
的值; ,求
,求 ,常数
,常数 ,若
,若 的图象与
的图象与 轴交于
轴交于 、
、 两点,线段
两点,线段 的中点为
的中点为 ,求证:
,求证: