题目内容
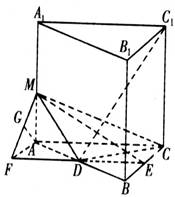
(本小题满分12分)如图，在直三棱柱ABC―A1B1C1中，∠ACB = 90°. AC = BC = a，
D、E分别为棱AB、BC的中点， M为棱AA1上的点，二面角M―DE―A为30°.
（1）求MA的长；w.w.w.k.s.5.u.c.o.m 
（2）求点C到平面MDE的距离。
解析：
（1） 过点A作CE的平行线，交ED的延长线于F，连结MF.
∵D、E分别为AB、BC的中点， ∴DE∥AC.
又∵AF∥CE，CE⊥AC，
∴AF⊥DE. ∵MA⊥平面ABC. ∴AF为MF在平面ABC内的射影，
∴MF⊥DE，∴∠MFA为二面角M―DE―A的平面角，∠MFA = 30°.
在Rt△MAF中，
，∠MFA = 30°，
∴
.………………6分w.w.w.k.s.5.u.c.o.m 
（2） 设C到平面MDE的距离为h.
∵
， ∴
，………8分
又∵
， 
，w.w.w.k.s.5.u.c.o.m
∴
， ∴
，即C到平面MDE的距离为
.…12分
练习册系列答案
同步练习强化拓展系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
