Question

 

1．   (本小题满分12分)

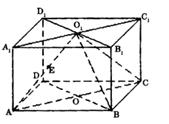
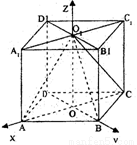
如图，直四棱柱ABCD—A₁B₁C₁D₁的高为3，底面是边长为4且∠DAB = 60°的菱形，AC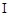BD = O，A₁C₁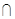B₁D₁ = O₁，E是O₁A的中点．

(1)  求二面角O₁－BC－D的大小；

(2)  求点E到平面O₁BC的距离．

 

 

 

 

 

 

 

 

 

Answer 1

【答案】

60°，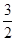

【解析】

解法一：

(1) 过O作OF⊥BC于F，连接O₁F，

∵OO₁⊥面AC，∴BC⊥O₁F，

∴∠O₁FO是二面角O₁－BC－D的平面角，········ 3分

∵OB = 2，∠OBF = 60°，∴OF =．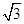

在Rt△O₁OF中，tan∠O₁FO =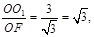

∴∠O₁FO=60° 即二面角O₁—BC—D的大小为60°············· 6分

(2) 在△O₁AC中，OE是△O₁AC的中位线，∴OE∥O₁C

∴OE∥O₁BC，∵BC⊥面O₁OF，∴面O₁BC⊥面O₁OF，交线O₁F．

过O作OH⊥O₁F于H，则OH是点O到面O₁BC的距离，··········· 10分

∴OH =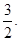 ∴点E到面O₁BC的距离等于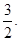················ 12分

解法二：

(1) ∵OO₁⊥平面AC，

∴OO₁⊥OA，OO₁⊥OB，又OA⊥OB，········· 2分

建立如图所示的空间直角坐标系（如图）

∵底面ABCD是边长为4，∠DAB = 60°的菱形，

∴OA = 2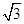，OB = 2，

则A（2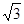，0，0），B（0，2，0），C（－2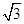，0，0），O₁（0，0，3）··· 3分

设平面O₁BC的法向量为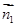=（x，y，z），则⊥，⊥，

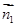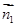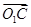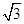∴，则z = 2，则x=－，y = 3，

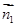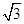∴=（－，3，2），而平面AC的法向量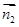=（0，0，3）········ 5分

∴ cos<，>=，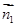

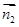设O₁－BC－D的平面角为α， ∴cosα=∴α=60°．

故二面角O₁－BC－D为60°．······················ 6分

(2) 设点E到平面O₁BC的距离为d，

    ∵E是O₁A的中点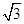，∴=（－，0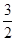，），············· 9分

则d=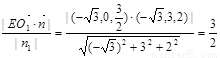

∴点E到面O₁BC的距离等于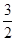．···················· 12分