摘要:20. 解法一: (Ⅰ)因AB⊥面BB1C1C.故AB⊥BE. 又EB1⊥EA.且EA在面BCC1B1内的射影为EB. 由三垂线定理的逆定理知EB1⊥BE.因此BE是异面直线 AB与EB1的公垂线. 在平行四边形BCC1B1中.设EB=x.则EB1=. 作BD⊥CC1.交CC1于D.则BD=BC· 在△BEB1中.由面积关系得. 解之得CE=2.故此时E与C1重合.由题意舍去. 因此x=1.即异面直线AB与EB1的距离为1. (Ⅱ)过E作EG//B1A1.则GE⊥面BCC1B.故GE⊥EB1且GE在圆A1B1E内. 又已知AE⊥EB1 故∠AEG是二面角A-EB1-A1的平面角. 因EG//B1A1//BA.∠AEG=∠BAE.故 解法二: (Ⅰ) 而BB1C1C得AB⊥EB1从而=0. 设O是BB1的中点.连接EO及OC1.则在Rt△BEB1中.EO=BB1=OB1=1. 因为在△OB1C1中.B1C1=1.∠OB1C1=.故△OB1C1是正三角形. 所以OC1=OB1=1. 又因∠OC1E=∠B1C1C-∠B1C1O=故△OC1E是正三角形. 所以C1E=1.故CE=1.易见△BCE是正三角形.从面BE=1. 即异面直线AB与EB1的距离是1. 可得∠AEB是二面角A-EB1-B的平面角.在Rt△ABE中.由AB=. BE=1.得tanAEB=. 又由已知得平面A1B1E⊥平面BB1C1C. 故二面角A-EB1-A1的平面角.故 解法三: (I)以B为原点..分别为y.z轴建立空间直角坐标系. 由于BC=1.BB1=2.AB=.∠BCC1=. 在三棱柱ABC-A1B1C1中有 B.A(0.0.).B1. 设 又AB⊥面BCC1B1.故AB⊥BE. 因此BE是异面直线AB.EB1的公垂线. 则.故异面直线AB.EB1的距离为1. (II)由已知有故二面角A-EB1-A1的平面角的大小为向量 的夹角.
网址:http://m.1010jiajiao.com/timu3_id_4468722[举报]
 分别是
分别是 的中点.
的中点. ;
; 的体积.
的体积.

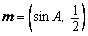 与
与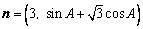 共线,其中A是△ABC的内角。
共线,其中A是△ABC的内角。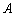 的大小;
的大小; 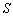 的最大值,并判断S取得最大值时△ABC的形状。
的最大值,并判断S取得最大值时△ABC的形状。 的直观图及其正视图、侧视图、俯视图如图所示.
的直观图及其正视图、侧视图、俯视图如图所示.  面
面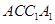 ; (2)求点
; (2)求点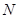 到平面
到平面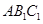 的距离;
的距离;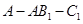 的大小.
的大小. 是矩形,
是矩形,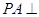 平面
平面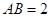 ,
, ,
,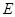 为
为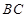 的中点.
的中点.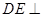 平面
平面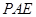 ;
; 与平面
与平面
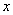 的不等式
的不等式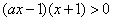 (
( )。
)。