摘要:有下列5个命题: ①数列0.1.0.-1与数列-1.0.1.0是相同的数列, ②数列中不能有相等的项, ③数列2.4.6.8-可表示为, ④数列1.3.5.2.-可表示为, ⑤数列1.2.3-不一定是无穷递增数列. 其中正确命题的个数为( ) A.1 B.2 C.3 D.4
网址:http://m.1010jiajiao.com/timu3_id_4467077[举报]
 给出下列5个命题:
给出下列5个命题:①0<a≤
| 1 |
| 5 |
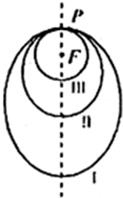
②如图所示,“嫦娥探月卫星”沿地月转移轨道飞向月球,在月球附近一点P进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道II绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道III绕月飞行,若用2Cl和2c2分别表示摘圆轨道I和II的焦距,用2a1和2a2分别表示椭圆轨道I和II的长轴的长,则有c1a2>a1c2;
③函数y=f(x)与它的反函数y=f-1(x)的图象若相交,则交点必在直线y=x上;
④己知函数f(x)=loga(1-ax)在(O,1)上满足,f′(x)>0,贝U
| 1 |
| 1-a |
| 2a |
⑤函数f(x)=
tan2x+
| ||
|
| π |
| 2 |
其中所有真命题的代号是
给出下列四个命题:
(1)函数y=3sin
+4cos
的定义域为[0,2π],则值域为[-5,5];
(2)三角方程tan(5x+
)=
在[0,π]内有5个解;
(3)对任意的α∈R,三角公式sin2α=
是一定成立的;
(4)函数y=cosx与y=arccosx(|x|≤1)互为反函数.
其中正确的个数是( )
(1)函数y=3sin
| x |
| 2 |
| x |
| 2 |
(2)三角方程tan(5x+
| 2π |
| 9 |
| 2 |
(3)对任意的α∈R,三角公式sin2α=
| 2tanα |
| 1+tan2α |
(4)函数y=cosx与y=arccosx(|x|≤1)互为反函数.
其中正确的个数是( )
查看习题详情和答案>>
给出下列4个命题:
①0<a≤
是f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为单调减函数的充要条件;
②函数f(x)=
(e是自然对数的底数)的最小值为2;
③y=f(x)与它的反函数y=f-1(x)的图象若相交,则交点必在直线y=x上;
④若α∈(π,
),则
>1+tanα>
;
其中所有假命题的代号有
查看习题详情和答案>>
①0<a≤
| 1 |
| 5 |
②函数f(x)=
| e-x+3 | ||
|
③y=f(x)与它的反函数y=f-1(x)的图象若相交,则交点必在直线y=x上;
④若α∈(π,
| 5π |
| 4 |
| 1 |
| 1-tanα |
| 2tanα |
其中所有假命题的代号有
①②③
①②③
. 恒有公共点,实数m的取值范围是m≥1
恒有公共点,实数m的取值范围是m≥1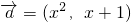 ,
,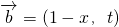 ,若函数f(x)=
,若函数f(x)= 在区间上是增函数,则实数t的取值范围是(5,+∞);
在区间上是增函数,则实数t的取值范围是(5,+∞); 恒有公共点,实数m的取值范围是m≥1
恒有公共点,实数m的取值范围是m≥1 ,
, ,若函数f(x)=
,若函数f(x)= 在区间上是增函数,则实数t的取值范围是(5,+∞);
在区间上是增函数,则实数t的取值范围是(5,+∞);