摘要： (1).若切点是Qn(an,ank).则切线方程是 当n=1时.切线过点P(1.0) 即.得,当n>1时.切线过点 即 得 所以数列是首项为,公比为的等比数列., (2) ------------ (3)设 则两式相减.得 . ------------
网址：http://m.1010jiajiao.com/timu3_id_4466745[举报]
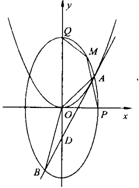已知点D（0，-2），过点D作抛线C1：x2=2py（p＞0）的切线l，切点A在第一象限，如图．（1）求切点A的纵坐标；
（2）若离心率为
| ||
| 2 |
| y2 |
| a 2 |
| x2 |
| b2 |
（3）设P、Q分别是（2）中的椭圆C2的右顶点和上顶点，M是椭圆C2在第一象限的任意一点，求四边形OPMQ面积的最大值以及此时M点的坐标． 查看习题详情和答案>>
已知函数f（x）=
，
（Ⅰ）求函数f（x）的单调区间和极值；
（Ⅱ）设P（x1，y1），Q（x2，y2）是函数f（x）图象上的两点且x1＜1，x2＞1，若直线PQ是函数f（x）图象的切线且P、Q都是切点，求证：3＜x2＜4；（参考数据：ln2≈0.6931，ln3≈1.0986）
（Ⅲ）设函数g（x）的定义域为D，区间I⊆D，若函数g（x）在I上可导，对任意的x0∈I，g（x）的图象在（x0，g（x0））处的切线为l，函数g（x）图象上所有的点都在直线l上方或直线l上，则称区间I为函数g（x）的“下线区间”．类比上面的定义，请你写出函数“上线区间”的定义，并根据你所给的定义，判断区间（-∞，
）是否是函数f（x）的“上线区间”（不必证明）．
查看习题详情和答案>>
|
（Ⅰ）求函数f（x）的单调区间和极值；
（Ⅱ）设P（x1，y1），Q（x2，y2）是函数f（x）图象上的两点且x1＜1，x2＞1，若直线PQ是函数f（x）图象的切线且P、Q都是切点，求证：3＜x2＜4；（参考数据：ln2≈0.6931，ln3≈1.0986）
（Ⅲ）设函数g（x）的定义域为D，区间I⊆D，若函数g（x）在I上可导，对任意的x0∈I，g（x）的图象在（x0，g（x0））处的切线为l，函数g（x）图象上所有的点都在直线l上方或直线l上，则称区间I为函数g（x）的“下线区间”．类比上面的定义，请你写出函数“上线区间”的定义，并根据你所给的定义，判断区间（-∞，
| 3 |
| 8 |
已知椭圆C：
+
=1(a＞b＞0)的长轴长是短轴长的
倍，F1，F2是它的左，右焦点．
（1）若P∈C，且
•
2=0，|PF1|•|PF2|=4，求F1、F2的坐标；
（2）在（1）的条件下，过动点Q作以F2为圆心、以1为半径的圆的切线QM（M是切点），且使|QF_|=
|QM|，求动点Q的轨迹方程．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
（1）若P∈C，且
| PF1 |
| PF |
（2）在（1）的条件下，过动点Q作以F2为圆心、以1为半径的圆的切线QM（M是切点），且使|QF_|=
| 2 |
已知定点O（0，0），A（3，0），动点P到定点O距离与到定点A的距离的比值是