ĢāÄæÄŚČŻ
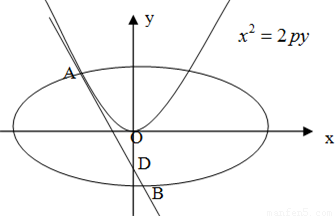
 ŅŃÖŖµćD£Ø0£¬-2£©£¬¹żµćD×÷Å×ĻßC1£ŗx2=2py£Øp£¾0£©µÄĒŠĻßl£¬ĒŠµćAŌŚµŚŅ»ĻóĻŽ£¬ČēĶ¼£®
ŅŃÖŖµćD£Ø0£¬-2£©£¬¹żµćD×÷Å×ĻßC1£ŗx2=2py£Øp£¾0£©µÄĒŠĻßl£¬ĒŠµćAŌŚµŚŅ»ĻóĻŽ£¬ČēĶ¼£®£Ø1£©ĒóĒŠµćAµÄׯ×ų±ź£»
£Ø2£©ČōĄėŠÄĀŹĪŖ
| ||
| 2 |
| y2 |
| a 2 |
| x2 |
| b2 |
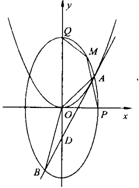
£Ø3£©ÉčP”¢Q·Ö±šŹĒ£Ø2£©ÖŠµÄĶÖŌ²C2µÄÓŅ¶„µćŗĶÉĻ¶„µć£¬MŹĒĶÖŌ²C2ŌŚµŚŅ»ĻóĻŽµÄČĪŅāŅ»µć£¬ĒóĖıߊĪOPMQĆ껿µÄ×ī“óÖµŅŌ¼°“ĖŹ±MµćµÄ×ų±ź£®
·ÖĪö£ŗ£Ø1£©ÉčĒŠµćAµÄ×ų±ź£¬µĆĒŠĻߵķ½³Ģ£¬øł¾ŻµćD£Ø0£¬-2£©ŌŚlÉĻ£¬“Ó¶ųæÉĒóĒŠµćAµÄׯ×ų±ź£»
£Ø2£©ÓÉe=
µĆa2=4b2£¬“Ó¶ųÓŠĶÖŌ²·½³ĢĪŖ
+
=1£¬½«Ö±ĻßÓėĶÖŌ²ĮŖĮ¢
µĆ£Øk2+4£©x2-4kx+4-4b2=0£¬ĄūÓĆ2k1+k2=3kæÉĒóÅ×ĪļĻßC1ŗĶĶÖŌ²C2µÄ·½³Ģ£®
£Ø3£©ÉčM£Øm£¬n£©£Øm£¬n£¾0£©£¬Ōņ4m2+n2=20£¬±ķŹ¾³öĖıߊĪOPMQĆ껿£¬ĄūÓĆ»ł±¾²»µČŹ½Ēó×ī“óÖµ£¬“Ó¶ųĒó³öMµÄ×ų±ź£®
£Ø2£©ÓÉe=
| ||
| 2 |
| y2 |
| 4b2 |
| x2 |
| b2 |
|
£Ø3£©ÉčM£Øm£¬n£©£Øm£¬n£¾0£©£¬Ōņ4m2+n2=20£¬±ķŹ¾³öĖıߊĪOPMQĆ껿£¬ĄūÓĆ»ł±¾²»µČŹ½Ēó×ī“óÖµ£¬“Ó¶ųĒó³öMµÄ×ų±ź£®
½ā“š£ŗ½ā£ŗ£Ø1£©ÉčĒŠµćA(x1£¬ y1)£¬y1=
£¬ĒŠĻߵķ½³ĢĪŖx1x=p£Øy1+y£©£¬ÓÖµćD£Ø0£¬-2£©ŌŚlÉĻ£¬ĖłŅŌy1=2£¬¼“ĒŠµćAµÄׯ×ų±źĪŖ2£»
£Ø2£©ÓÉ£Ø1£©µĆA(2
£¬2)£¬ĒŠĻߊ±ĀŹk=
¢Ł£¬ÉčB£Øx2£¬y2£©£¬ĒŠĻß·½³Ģy=kx-2£¬ÓÉe=
µĆa2=4b2£¬”ąĶÖŌ²·½³ĢĪŖ
+
=1ĒŅ¹żµćA(2
£¬2)
ÓÉ
µĆ£Øk2+4£©x2-4kx+4-4b2=0£¬”ą
¢Ś
ÓÉ2k1+k2=3kæɵĆ2x1+4x2=0£¬”ąx1=2
£¬x2=-
“śČė¢Ś½āµĆk=2£¬b2=5£¬”ąa2=20£¬”ąp=1
ĖłŅŌÅ×ĪļĻßC1µÄ·½³ĢĪŖx2=2y£¬ĶÖŌ²C2µÄ·½³Ģ
+
=1
£Ø3£©ÉčM£Øm£¬n£©£Øm£¬n£¾0£©£¬Ōņ4m2+n2=20£¬S=
(
m+
n)=
(2m+n)ӆ
”Į
=
£¬µ±ĒŅ½öµ±2m=n£¬¼“m=
£¬n=
Ź±£¬Č””°=”±£¬¹ŹĖıߊĪOPMQĆ껿µÄ×ī“óÖµĪŖ
£¬MµÄ×ų±źĪŖ(
£¬
)
| ||
| 2p |
£Ø2£©ÓÉ£Ø1£©µĆA(2
| p |
| 2 | ||
|
| ||
| 2 |
| y2 |
| 4b2 |
| x2 |
| b2 |
| p |
ÓÉ
|
|
ÓÉ2k1+k2=3kæɵĆ2x1+4x2=0£¬”ąx1=2
| p |
| p |
ĖłŅŌÅ×ĪļĻßC1µÄ·½³ĢĪŖx2=2y£¬ĶÖŌ²C2µÄ·½³Ģ
| y2 |
| 20 |
| x2 |
| 5 |
£Ø3£©ÉčM£Øm£¬n£©£Øm£¬n£¾0£©£¬Ōņ4m2+n2=20£¬S=
| 1 |
| 2 |
| 20 |
| 5 |
| ||
| 2 |
| ||
| 2 |
| 10 |
| 5 |
| 2 |
| 2 |
| ||
| 2 |
| 10 |
| 5 |
| 2 |
| 2 |
| ||
| 2 |
| 10 |
µćĘĄ£ŗ±¾ĢāÖ÷ŅŖæ¼²éÅ×ĪļĻßµÄĒŠĻß·½³Ģ£¬æ¼²éÖ±ĻßÓėĶÖŌ²µÄĪ»ÖĆ¹ŲĻµ¼°ĄūÓĆ»ł±¾²»µČŹ½ĒóĆ껿µÄ×īÖµ£®

Į·Ļ°²įĻµĮŠ“š°ø
 ÖŠæ¼½ā¶Įæ¼µć¾«Į·ĻµĮŠ“š°ø
ÖŠæ¼½ā¶Įæ¼µć¾«Į·ĻµĮŠ“š°ø
Ļą¹ŲĢāÄæ
 ŅŃÖŖµćD£Ø0£¬-2£©£¬¹żµćD×÷Å×ĪļĻßC1£ŗx2=2py£Øp£¾0£©µÄĒŠĻßl£¬ĒŠµćAŌŚµŚ¶žĻóĻŽ£¬ČēĶ¼
ŅŃÖŖµćD£Ø0£¬-2£©£¬¹żµćD×÷Å×ĪļĻßC1£ŗx2=2py£Øp£¾0£©µÄĒŠĻßl£¬ĒŠµćAŌŚµŚ¶žĻóĻŽ£¬ČēĶ¼ £Ø2012•»ĘÖŻĒųÄ£Äā£©ČēĶ¼£¬ŅŃÖŖµćD£Ø0£¬-2£©£¬¹żµćD×÷Å×ĪļĻßC1£ŗx2=2py£Øp”Ź[1£¬4]µÄĒŠĻßl£¬ĒŠµćAŌŚµŚ¶žĻóĻŽ£®
£Ø2012•»ĘÖŻĒųÄ£Äā£©ČēĶ¼£¬ŅŃÖŖµćD£Ø0£¬-2£©£¬¹żµćD×÷Å×ĪļĻßC1£ŗx2=2py£Øp”Ź[1£¬4]µÄĒŠĻßl£¬ĒŠµćAŌŚµŚ¶žĻóĻŽ£®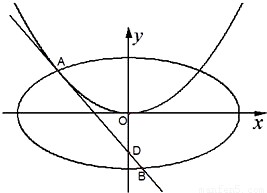 ŅŃÖŖµćD£Ø0£¬-2£©£¬¹żµćD×÷Å×ĪļĻßC1£ŗx2=2py£Øp£¾0£©µÄĒŠĻßl£¬ĒŠµćAŌŚµŚ¶žĻóĻŽ£¬ČēĶ¼
ŅŃÖŖµćD£Ø0£¬-2£©£¬¹żµćD×÷Å×ĪļĻßC1£ŗx2=2py£Øp£¾0£©µÄĒŠĻßl£¬ĒŠµćAŌŚµŚ¶žĻóĻŽ£¬ČēĶ¼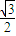 µÄĶÖŌ²
µÄĶÖŌ²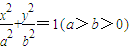 Ē”ŗĆ¾¹żĒŠµćA£¬ÉčĒŠĻßl½»ĶÖŌ²µÄĮķŅ»µćĪŖB£¬¼ĒĒŠĻßl£¬OA£¬OBµÄŠ±ĀŹ·Ö±šĪŖk£¬k1£¬k2£¬Čōk1+2k2=4k£¬ĒóĶÖŌ²·½³Ģ£®
Ē”ŗĆ¾¹żĒŠµćA£¬ÉčĒŠĻßl½»ĶÖŌ²µÄĮķŅ»µćĪŖB£¬¼ĒĒŠĻßl£¬OA£¬OBµÄŠ±ĀŹ·Ö±šĪŖk£¬k1£¬k2£¬Čōk1+2k2=4k£¬ĒóĶÖŌ²·½³Ģ£®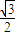 µÄĶÖŌ²
µÄĶÖŌ²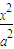 +
+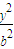 =1£Øa£¾b£¾c£©Ē”ŗĆ¾¹żAµć£¬ÉčĒŠĻßl½»ĶÖŌ²µÄĮķŅ»µćĪŖB£¬ČōÉčĒŠĻßl£¬Ö±ĻßOA£¬OBµÄŠ±ĀŹĪŖk£¬k1£¬k2£¬¢ŁŹŌÓĆŠ±ĀŹk±ķŹ¾k1+k2¢Śµ±k1+k2Č”µĆ×ī“óÖµŹ±Ēó“ĖŹ±ĶÖŌ²µÄ·½³Ģ£®
=1£Øa£¾b£¾c£©Ē”ŗĆ¾¹żAµć£¬ÉčĒŠĻßl½»ĶÖŌ²µÄĮķŅ»µćĪŖB£¬ČōÉčĒŠĻßl£¬Ö±ĻßOA£¬OBµÄŠ±ĀŹĪŖk£¬k1£¬k2£¬¢ŁŹŌÓĆŠ±ĀŹk±ķŹ¾k1+k2¢Śµ±k1+k2Č”µĆ×ī“óÖµŹ±Ēó“ĖŹ±ĶÖŌ²µÄ·½³Ģ£®