题目内容
 已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是
已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是| 1 | ||
|
(Ⅰ)求动点P的轨迹方程,并说明方程表示的曲线;
(Ⅱ)当λ=4时,记动点P的轨迹为曲线D.
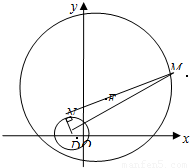
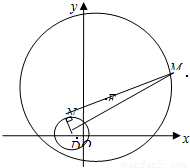
①若M是圆E:(x-2)2+(y-4)2=64上任意一点,过M作曲线D的切线,切点是N,求|MN|的取值范围;
②已知F,G是曲线D上不同的两点,对于定点Q(-3,0),有|QF|•|QG|=4.试问无论F,G两点的位置怎样,直线FG能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.
分析:(Ⅰ)设动点坐标,利用动点P到定点O距离与到定点A的距离的比值是
,建立方程,化简即可得到动点P的轨迹方程,从而可得方程表示的曲线;
(Ⅱ)当λ=4时,确定动点P的轨迹方程.
①确定两圆内含,且圆D在圆E内部.由|MN|2=|MD|2-|DN|2有:|MN|2=|MD|2-4,故求|MN|的取值范围就是求|MD|的取值范围;
②解法一:设点Q到直线FG的距离为d,∠FQG=θ,由面积相等得到顶点Q到动直线FG的距离为定值,从而可得结论;
解法二:假设存在,设出直线方程,利用直线与圆相切,得出圆心到直线的距离等于半径,即可得到结论.
| 1 | ||
|
(Ⅱ)当λ=4时,确定动点P的轨迹方程.
①确定两圆内含,且圆D在圆E内部.由|MN|2=|MD|2-|DN|2有:|MN|2=|MD|2-4,故求|MN|的取值范围就是求|MD|的取值范围;
②解法一:设点Q到直线FG的距离为d,∠FQG=θ,由面积相等得到顶点Q到动直线FG的距离为定值,从而可得结论;
解法二:假设存在,设出直线方程,利用直线与圆相切,得出圆心到直线的距离等于半径,即可得到结论.
解答:解:(Ⅰ)设动点P的坐标为(x,y),则由
|PO|=|PA|,得λ(x2+y2)=(x-3)2+y2,
整理得:(λ-1)x2+(λ-1)y2+6x-9=0.
∵λ>0,∴当λ=1时,则方程可化为:2x-3=0,故方程表示的曲线是线段OA的垂直平分线;
当λ≠1时,则方程可化为(x+
)2+y2=[
]2,即方程表示的曲线是以(-
,0)为圆心,
为半径的圆.…5分
(Ⅱ)当λ=4时,曲线D的方程是x2+y2+2x-3=0,故曲线D表示圆,圆心是D(-1,0),半径是2.
①由|DE|=
=5,及5<8-2有:两圆内含,且圆D在圆E内部.
如图所示,由|MN|2=|MD|2-|DN|2有:|MN|2=|MD|2-4,故求|MN|的取值范围就是求|MD|的取值范围.
而D是定点,M是圆上的动点,故过D作圆E的直径,得|MD|min=8-5=3,|MD|max=8+5=13,故5≤|MN|2≤165,
≤|MN|≤
.…9分
②解法一:设点Q到直线FG的距离为d,∠FQG=θ,
则由面积相等得到|QF|•|QG|sinθ=d|FG|,且圆的半径r=2.
即d=
=
=1.于是顶点Q到动直线FG的距离为定值,
即动直线FG与定圆(x+3)2+y2=1相切.
②解法二:设F,G两点的坐标分别为F(x1,y1),G(x2,y2),
则由|QF|•|QG|=4有:
•
=4,结合
+
+2x1-3=0,
+
+2x2-3=0有:
•
=4⇒x1x2+3(x 1+x2)+8=0,
若经过F、G两点的直线的斜率存在,设直线FG的方程为y=mx+n,
由
,消去y有:(1+m2)x2+(2mn+2)x+n2-3=0,则x1+x2=-
,x1x2=
=1,
所以x1x2+3(x 1+x2)+8=
+
+
=0,
由此可得8m2-6mn+n2=1,也即(3m-n)2=1+m2,
=1…(※).
假设存在定圆(x-a)2+(y-b)2=r2,总与直线FG相切,则
d=
是定值r,即d与m,n无关,与
=1…(※)对比,有
,
此时d=r=
=1,故存在定圆(x+3)2+y2=1,
当直线FG的斜率不存在时,x1=x2=-2,直线FG的方程是x=-2,显然和圆相切.
故直线FG能恒切于一个定圆(x+3)2+y2=1.…14分.
| λ |
整理得:(λ-1)x2+(λ-1)y2+6x-9=0.
∵λ>0,∴当λ=1时,则方程可化为:2x-3=0,故方程表示的曲线是线段OA的垂直平分线;
当λ≠1时,则方程可化为(x+
| 3 |
| λ-1 |
3
| ||
| (λ-1) |
| 3 |
| λ-1 |
3
| ||
| |λ-1| |
(Ⅱ)当λ=4时,曲线D的方程是x2+y2+2x-3=0,故曲线D表示圆,圆心是D(-1,0),半径是2.
①由|DE|=
| (2+1)2+(4-0)2 |
如图所示,由|MN|2=|MD|2-|DN|2有:|MN|2=|MD|2-4,故求|MN|的取值范围就是求|MD|的取值范围.

而D是定点,M是圆上的动点,故过D作圆E的直径,得|MD|min=8-5=3,|MD|max=8+5=13,故5≤|MN|2≤165,
| 5 |
| 165 |
②解法一:设点Q到直线FG的距离为d,∠FQG=θ,
则由面积相等得到|QF|•|QG|sinθ=d|FG|,且圆的半径r=2.
即d=
| 4sinθ |
| |FG| |
| 4sinθ |
| 2rsinθ |
即动直线FG与定圆(x+3)2+y2=1相切.
②解法二:设F,G两点的坐标分别为F(x1,y1),G(x2,y2),
则由|QF|•|QG|=4有:
(x1+3)2+
|
(x2+3)2+
|
| x | 2 1 |
| y | 2 1 |
| x | 2 2 |
| y | 2 2 |
| 4x1+12 |
| 4x2+12 |
若经过F、G两点的直线的斜率存在,设直线FG的方程为y=mx+n,
由
|
| 2mn+2 |
| 1+m2 |
| n2 |
| 1+m2 |
所以x1x2+3(x 1+x2)+8=
| n2-3 |
| 1+m2 |
| -6mn-6 |
| 1+m2 |
| 1+8m2 |
| 1+m2 |
由此可得8m2-6mn+n2=1,也即(3m-n)2=1+m2,
| |3m-n| | ||
|
假设存在定圆(x-a)2+(y-b)2=r2,总与直线FG相切,则
d=
| |ma-b+n| | ||
|
| |3m-n| | ||
|
|
此时d=r=
| |3m-n| | ||
|
当直线FG的斜率不存在时,x1=x2=-2,直线FG的方程是x=-2,显然和圆相切.
故直线FG能恒切于一个定圆(x+3)2+y2=1.…14分.
点评:本题考查轨迹方程,考查圆与圆、直线与圆的位置关系,考查探索性问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 (2007•深圳一模)已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足
(2007•深圳一模)已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足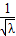 .
.
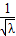 .
.