摘要：10．Sn表示数列{an}前n项的和.若对任意n∈N.恒有9Sn=10an+9(n+10).则通项公式an=

网址：http://m.1010jiajiao.com/timu3_id_4465922[举报]

若数列{a_n}前n项和为S_n（n∈N*）
（1）若首项a₁=1，且对于任意的正整数n（n≥2）均有

，（其中k为正实常数），试求出数列{a_n}的通项公式．
（2）若数列{a_n}是等比数列，公比为q，首项为a₁，k为给定的正实数，满足：
①a₁＞0，且0＜q＜1
②对任意的正整数n，均有S_n-k＞0；
试求函数f（n）=

的最大值（用a₁和k表示）

查看习题详情和答案>>

已知数列{a_n}的前n项和为S_n，且对任意正整数n，有S_n，

an，n（a≠0，a≠1）成等差数列，令b_n=（a_n+1）lg（a_n+1）．
（1）求数列{a_n}的通项公式a_n（用a，n表示）
（2）当a=

时，数列{b_n}是否存在最小项，若有，请求出第几项最小；若无，请说明理由；
（3）若{b_n}是一个单调递增数列，请求出a的取值范围．查看习题详情和答案>>

已知数列{a_n}的前n项和为S_n且对任意正整数n总有S_n=p（a_n-1）（p为常数，且p≠0，p≠1），数列{b_n}满足
b_n=kn+q（q为常数）
（1）求数列{a_n}的首项a₁及通项公式（用p表示）；
（2）若恰好存在唯一实数p使得a₁=b₁，a₃=b₃，求实数k的取值的集合．查看习题详情和答案>>

已知数列{a_n}的前n项和为S_n，且对任意正整数n总有S_n=p（a_n-1）（p为常数，且p≠0，p≠1），数列{b_n}满足b_n=2n+q（q为常数）
（I）求数列{a_n}的通项公式（用p表示）；
（II）若a₁=b₁，a₂＜b₂，求p的取值范围．

查看习题详情和答案>>

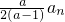已知数列{a_n}的前n项和为S_n，且对任意正整数n，有S_n， $数学公式$ ，n（a≠0，a≠1）成等差数列，令b_n=（a_n+1）lg（a_n+1）．
（1）求数列{a_n}的通项公式a_n（用a，n表示）
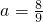（2）当 $数学公式$ 时，数列{b_n}是否存在最小项，若有，请求出第几项最小；若无，请说明理由；
（3）若{b_n}是一个单调递增数列，请求出a的取值范围．

查看习题详情和答案>>