题目内容
已知数列{an}的前n项和为Sn且对任意正整数n总有Sn=p(an-1)(p为常数,且p≠0,p≠1),数列{bn}满足bn=kn+q(q为常数)
(1)求数列{an}的首项a1及通项公式(用p表示);
(2)若恰好存在唯一实数p使得a1=b1,a3=b3,求实数k的取值的集合.
分析:(1)先把n=1直接代入求出数列{an}的首项a1,再利用an=Sn-Sn-1 (n≥2)找到递推关系式整理即可求通项公式;
(2)先把已知条件代入整理为(
)3-
=2k,再借助于函数f(x)=x3-xx≠0且x≠1的图象来求实数k的取值的集合.
(2)先把已知条件代入整理为(
| p |
| p-1 |
| p |
| p-1 |
解答: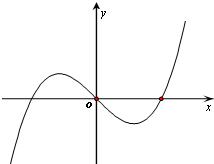
解:(1)由题a1=s1=p(a1-1)?a1=
(p≠0,p≠1),
当n≥2时,an=sn-sn-1=p(an-an-1)?(p-1)an=pan-1,
即
=
(常数).
所以{an}是以
为首项,
为公比的等比数列,
所以an=
• (
) n-1= (
)n
(2)
?
?(
)3=2k+
?(
)3-
=2k,
考虑函数f(x)=x3-xx≠0且x≠1
则f'(x)=3x2-1=3(x+
)(x-
)
所以f(x)=x3-xx≠0且x≠1,在(-∞,-
),(
,1),(1,+∞)上为增函数;
在(-
,
)上为减函数;
恰好存在唯一实数p使得a1=b1,a3=b3,
只要方程x3-x=2k恰有一个实数解.
由图象可知,实数k的取值的集合为(-∞,-
)∪{0}∪(
,+∞).

解:(1)由题a1=s1=p(a1-1)?a1=
| p |
| p-1 |
当n≥2时,an=sn-sn-1=p(an-an-1)?(p-1)an=pan-1,
即
| an |
| an-1 |
| p |
| p-1 |
所以{an}是以
| p |
| p-1 |
| p |
| p-1 |
所以an=
| p |
| p-1 |
| p |
| p-1 |
| p |
| p-1 |
(2)
|
|
| p |
| p-1 |
| p |
| p-1 |
| p |
| p-1 |
| p |
| p-1 |
考虑函数f(x)=x3-xx≠0且x≠1
则f'(x)=3x2-1=3(x+
| ||
| 3 |
| ||
| 3 |
所以f(x)=x3-xx≠0且x≠1,在(-∞,-
| ||
| 3 |
| ||
| 3 |
在(-
| ||
| 3 |
| ||
| 3 |
恰好存在唯一实数p使得a1=b1,a3=b3,
只要方程x3-x=2k恰有一个实数解.
由图象可知,实数k的取值的集合为(-∞,-
2
| ||
| 9 |
2
| ||
| 9 |
点评:本题是对数列的递推关系式以及数列与函数综合的考查.本题第二问的关键点在与转化为求函数f(x)=x3-xx≠0且x≠1的取值,借助于其图象来求对应实数k的取值.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |