摘要： 下面四个函数中.以π为最小正周期.且在区间()上为减函数的是( ) A. B. C. D.
网址：http://m.1010jiajiao.com/timu3_id_4465613[举报]
（2012•济南三模）下面给出的四个命题中：
①以抛物线y2=4x的焦点为圆心，且过坐标原点的圆的方程为（x-1）2+y2=1；
②若m=-2，则直线（m+2）x+my+1=0与直线（m-2）x+（m+2）y-3=0相互垂直；
③命题“?x∈R，使得x2+3x+4=0”的否定是“?x∈R，都有x2+3x+4≠0”；
④将函数y=sin2x的图象向右平移
个单位，得到函数y=sin（2x-
）的图象．
其中是真命题的有
查看习题详情和答案>>
①以抛物线y2=4x的焦点为圆心，且过坐标原点的圆的方程为（x-1）2+y2=1；
②若m=-2，则直线（m+2）x+my+1=0与直线（m-2）x+（m+2）y-3=0相互垂直；
③命题“?x∈R，使得x2+3x+4=0”的否定是“?x∈R，都有x2+3x+4≠0”；
④将函数y=sin2x的图象向右平移
| π |
| 3 |
| π |
| 6 |
其中是真命题的有
①②③
①②③
（将你认为正确的序号都填上）．下表是芝加哥1951～1981年月平均气温（华氏）.
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
平均气温 | 21.4 | 26.0 | 36.0 | 48.8 | 59.1 | 68.6 |
月份 | 7 | 8 | 9 | 10 | 11 | 12 |
平均气温 | 73.0 | 71.9 | 64.7 | 53.5 | 39.8 | 27.7 |
(1)以月份为x轴，x=月份-1，以平均气温为y轴，描出散点图；
（2）用正弦曲线去拟合这些数据；
（3）这个函数的周期是多少？
（4）估计这个正弦曲线的振幅A；
（5）选择下面四个函数模型中哪一个最适合这些数据？
①
=cos(
);②
=cos(
);③
=cos(
);④
=sin(
).
下面给出的四个命题中：
①以抛物线y2＝4x的焦点为圆心，且过坐标原点的圆的方程为
；
②若
，则直线
与直线
相互垂直；
③命题 “
，使得
”的否定是“
，都有
”；
④将函数
的图象向右平移
个单位，得到函数
的图象。
其中是真命题的有 （将你认为正确的序号都填上）。
查看习题详情和答案>>
下面给出的四个命题中：
①以抛物线y2=4x的焦点为圆心，且过坐标原点的圆的方程为（x-1）2+y2=1；
②若m=-2，则直线（m+2）x+my+1=0与直线（m-2）x+（m+2）y-3=0相互垂直；
③命题“?x∈R，使得x2+3x+4=0”的否定是“?x∈R，都有x2+3x+4≠0”；
④将函数y=sin2x的图象向右平移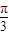
个单位，得到函数y=sin（2x-
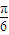）的图象．
其中是真命题的有 （将你认为正确的序号都填上）． 查看习题详情和答案>>
①以抛物线y2=4x的焦点为圆心，且过坐标原点的圆的方程为（x-1）2+y2=1；
②若m=-2，则直线（m+2）x+my+1=0与直线（m-2）x+（m+2）y-3=0相互垂直；
③命题“?x∈R，使得x2+3x+4=0”的否定是“?x∈R，都有x2+3x+4≠0”；
④将函数y=sin2x的图象向右平移
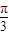个单位，得到函数y=sin（2x-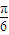）的图象．其中是真命题的有 （将你认为正确的序号都填上）． 查看习题详情和答案>>
下表是芝加哥从1978年到2008年的月平均气温(华氏)．
(1)以月份为x轴，x＝月份－1，以平均气温为y轴，描出散点图；
(2)用正弦曲线去拟合这些数据；
(3)这个函数的周期是多少？
(4)估计这个正弦曲线的振幅A(精确到度)；
(5)下面四个函数模型中哪一个最适合这些数据？
[ ]
|
A． |
B． |
|
C． |
D． |
；
；
；
；(6)请再写出一个与(5)中所选答案等价的模型来描述这些数据．
查看习题详情和答案>>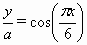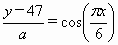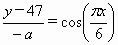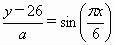