题目内容
下表是芝加哥从1978年到2008年的月平均气温(华氏).

(1)以月份为x轴,x=月份-1,以平均气温为y轴,描出散点图;
(2)用正弦曲线去拟合这些数据;
(3)这个函数的周期是多少?
(4)估计这个正弦曲线的振幅A(精确到度);
(5)下面四个函数模型中哪一个最适合这些数据?
[ ]
|
A. |
B. |
|
C. |
D. |
(6)请再写出一个与(5)中所选答案等价的模型来描述这些数据.
答案:略
解析:
解析:
|
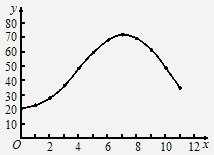
(1)、(2)如图.
(3)12.(4)约26( |

练习册系列答案
相关题目
下表是芝加哥1951~1981年月平均气温(华氏).
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
平均气温 | 21.4 | 26.0 | 36.0 | 48.8 | 59.1 | 68.6 |
月份 | 7 | 8 | 9 | 10 | 11 | 12 |
平均气温 | 73.0 | 71.9 | 64.7 | 53.5 | 39.8 | 27.7 |
(1)以月份为x轴,x=月份-1,以平均气温为y轴,描出散点图;
(2)用正弦曲线去拟合这些数据;
(3)这个函数的周期是多少?
(4)估计这个正弦曲线的振幅A;
(5)选择下面四个函数模型中哪一个最适合这些数据?
①![]() =cos(
=cos(![]() );②
);②![]() =cos(
=cos(![]() );③
);③![]() =cos(
=cos(![]() );④
);④![]() =sin(
=sin(![]() ).
).
随着居民收入的增加,私家车的拥有量呈快速增长趋势,下表是A市2008年以来私家车拥有量的调查数据:
(Ⅰ)甲、乙两同学利用统计知识对以上数据进行处理,得到的线性回归方程为甲: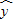 =3.5x+5,乙:
=3.5x+5,乙: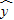 =3.2x+3.6.已知甲、乙中只有一人计算正确,请判断哪位同学的结论正确,并说明理由;
=3.2x+3.6.已知甲、乙中只有一人计算正确,请判断哪位同学的结论正确,并说明理由;
(Ⅱ)在(Ⅰ)前提下,请估计2013年该城市私家车的拥有量.
| 年份2008+x(年) | 1 | 2 | 3 | 4 | |
| 私家车拥有量y(万辆) | 5 | 7 | 8 | 11 | 19 |
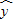 =3.5x+5,乙:
=3.5x+5,乙: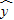 =3.2x+3.6.已知甲、乙中只有一人计算正确,请判断哪位同学的结论正确,并说明理由;
=3.2x+3.6.已知甲、乙中只有一人计算正确,请判断哪位同学的结论正确,并说明理由;(Ⅱ)在(Ⅰ)前提下,请估计2013年该城市私家车的拥有量.
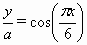 ;
;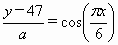 ;
;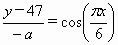 ;
;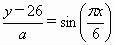 ;
;
 ).(5)C.(6)例如:
).(5)C.(6)例如: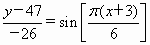 .
.