摘要： 设表示平面,表示直线且,给出四个论断: ①∥;②∥;③;④,若以其中三个论断作条件,余下一个作结论,可构造出四个命题,写出你认为正确的一个命题 .﹑( ) 填上论断的序号即可.) 三﹑解答题(本大题共6小题,共74分,解答要写出文字说明,证明过程或演算步骤)
网址：http://m.1010jiajiao.com/timu3_id_4465437[举报]
设m、l是两条异面直线,α、β表示平面,请把下列命题中正确命题的代号全部填在横线上___________________.
①当α-l-β是直二面角时,若m⊥l,则m⊥β②若m⊥α,l⊥β,m⊥l,则α⊥β③若m⊥α,l⊥β,则α、β必相交④存在唯一的平面α与m、l等距离
查看习题详情和答案>>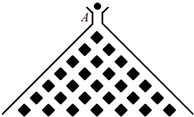
（2011•丹东模拟）如图，在竖直平面内有一个“游戏滑道”，空白部分表示光滑滑道，黑色正方形表示障碍物，自上而下第一行有1个障碍物，第二行有2个障碍物，…，依此类推．一个半径适当的光滑均匀小球从入口A投入滑道，小球将自由下落，已知小球每次遇到正方形障碍物上顶点时，向左、右两边下落的概率都是| 1 |
| 2 |
（Ⅰ）求P（4，1），P（4，2）的值，并猜想P（n，m）的表达式（不必证明）；
（Ⅱ）已知f（x）=
|
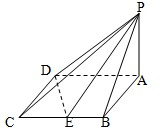如图四棱锥P-ABCD的底面是边长为2的菱形，且∠BAD=60°，PA⊥平面ABCD，设E为BC的中点，二面角P-DE-A为45°．（1 ） 求点A到平面PDE的距离；
（2 ） 在PA上确定一点F，使BF∥平面PDE；
（3 ） 求平面PDE与平面PAB所成的不大于直二面角的二面角的大小（用反三角函数表示）．
如图是在竖直平面内的一个“通道游戏”．图中竖直线段和斜线段都表示通道，并且在交点处相遇，若竖直线段有第一条的为第一层，有二条的为第二层，…，依此类推．现有一颗小弹子从第一层的通道里向下运动．记小弹子落入第n层第m个竖直通道（从左至右）的概率为P（n，m）．（已知在通道的分叉处，小弹子以相同的概率落入每个通道）