题目内容
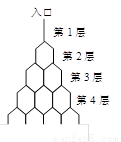
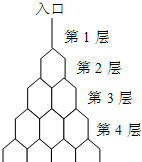 如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道)(Ⅰ)求P(2,1),P(3,2)的值,并猜想P(n,m)的表达式.(不必证明)
(Ⅱ)设小弹子落入第6层第m个竖直通道得到分数为ξ,其中ξ=
|
分析:(Ⅰ)根据小弹子以相同的概率落入每个通道,在每一个分叉处小球落入那一个通道的概率是相同的,根据独立重复试验的概率公式得到结果,推出具有一般性的结论.
(Ⅱ)根据题意知变量ξ的可能取值是3,2,1,结合变量对应的事件和前一问做出的概率公式,写出变量对应的概率和分布列,求出期望值.
(Ⅱ)根据题意知变量ξ的可能取值是3,2,1,结合变量对应的事件和前一问做出的概率公式,写出变量对应的概率和分布列,求出期望值.
解答:解:(Ⅰ)由题意知,
P(2,1)=
(
)0(
)1=
P(3,2)=
(
)1(
)1=
∴P(m,n)=
(Ⅱ)由题意知变量ξ的可能取值是3,2,1
P(ξ=3)=
=
,
P(ξ=2)=
=
,
P(ξ=1)=
=
∴ξ的分布列是
∴Eξ=3×
+2×
+1×
=
P(2,1)=
| C | 0 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
P(3,2)=
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴P(m,n)=
| ||
| 2n-1 |
(Ⅱ)由题意知变量ξ的可能取值是3,2,1
P(ξ=3)=
2
| ||
| 25 |
| 2 |
| 32 |
P(ξ=2)=
| ||
| 25 |
| 10 |
| 32 |
P(ξ=1)=
2
| ||
| 25 |
| 20 |
| 32 |
∴ξ的分布列是
| ξ | 3 | 2 | 1 | ||||||
| P |
|
|
|
| 2 |
| 32 |
| 10 |
| 32 |
| 20 |
| 32 |
| 23 |
| 16 |
点评:本题考查离散型随机变量的分布列和期望,考查独立重复试验的概率公式,考查归纳推理,本题的题意比较好,容易引起学生的兴趣.

练习册系列答案
相关题目
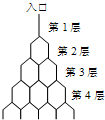 如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道)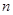 层第
层第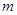 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为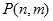 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第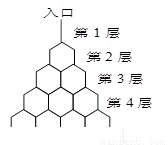
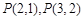 及
及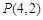 的值,并猜想
的值,并猜想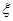 ,其中
,其中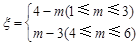 ,试求
,试求 层第
层第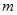 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第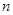 层的第
层的第 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.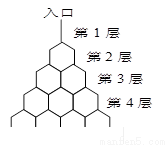
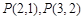 及
及 的值,并猜想
的值,并猜想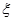 ,其中
,其中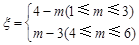 ,试求
,试求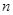 层第
层第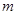 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为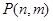 .(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
.(已知在通道的分叉处,小弹子以相同的概率落入每个通道)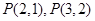 的值,并猜想
的值,并猜想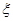 ,其中
,其中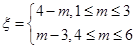 ,试求
,试求