题目内容
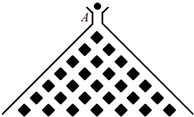 (2011•丹东模拟)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
(2011•丹东模拟)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是| 1 |
| 2 |
(Ⅰ)求P(4,1),P(4,2)的值,并猜想P(n,m)的表达式(不必证明);
(Ⅱ)已知f(x)=
|
分析:(I)根据已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
,小球遇到第n行第m个障碍物(从左至右)上顶点的概率为P(n,m),可得P(4,1),P(4,2),可以猜想P(n,m);
(II)ξ的可能取值为3,2,1,求出相应概率,可得分布列,从而可得期望.
| 1 |
| 2 |
(II)ξ的可能取值为3,2,1,求出相应概率,可得分布列,从而可得期望.
解答:解:(I)根据已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
,小球遇到第n行第m个障碍物(从左至右)上顶点的概率为P(n,m),可得P(4,1)=
(
)3=
,P(4,2)=
(
)3=
猜想P(n,m)=
(
)n-1; …(6分)
(II)ξ的可能取值为3,2,1,…(7分)
P(ξ=3)=P(6,1)+P(6,6)=
,P(ξ=2)=P(6,2)+P(6,5)=
(
)5=
,P(ξ=1)=P(6,3)+P(6,4)=
分布列为:
…(10分)
Eξ=3×
+2×
+1×
=
. …(12分)
| 1 |
| 2 |
| C | 0 3 |
| 1 |
| 2 |
| 1 |
| 8 |
| C | 1 3 |
| 1 |
| 2 |
| 3 |
| 8 |
猜想P(n,m)=
| C | m-1 n-1 |
| 1 |
| 2 |
(II)ξ的可能取值为3,2,1,…(7分)
P(ξ=3)=P(6,1)+P(6,6)=
| 1 |
| 16 |
| C | 1 5 |
| 1 |
| 2 |
| 5 |
| 16 |
| 5 |
| 8 |
分布列为:
| ξ | 3 | 2 | 1 | ||||||
| P |
|
|
|
Eξ=3×
| 1 |
| 16 |
| 5 |
| 16 |
| 5 |
| 8 |
| 23 |
| 16 |
点评:本题考查概率的计算,考查离散型随机变量的分布列与期望,解题的关键是确定变量的取值,求出相应的概率.

练习册系列答案
相关题目
 (2011•丹东模拟)选修4-1:几何证明选讲
(2011•丹东模拟)选修4-1:几何证明选讲