摘要：对于实数集A={x|}.B={x|}.是否存在实数a.使A∪B=Φ?如果存在.请求出!
网址：http://m.1010jiajiao.com/timu3_id_4464706[举报]
已知函数f（x）=ax-lnx+1（a∈R），g（x）=xe1-x．
（1）求函数g（x）在区间（0，e]上的值域T；
（2）是否存在实数a，对任意给定的集合T中的元素t，在区间[1，e]上总存在两个不同的xi（i=1，2），使得f（xi）=t成立、若存在，求出a的取值范围；若不存在，请说明理由；
（3 ）函数f（x）图象上是否存在两点A（x1，y1）和B（x2，y2），使得割线AB的斜率恰好等于函数f（x）在AB中点M（x0，y0）处切线的斜率？请写出判断过程．
查看习题详情和答案>>
（1）求函数g（x）在区间（0，e]上的值域T；
（2）是否存在实数a，对任意给定的集合T中的元素t，在区间[1，e]上总存在两个不同的xi（i=1，2），使得f（xi）=t成立、若存在，求出a的取值范围；若不存在，请说明理由；
（3 ）函数f（x）图象上是否存在两点A（x1，y1）和B（x2，y2），使得割线AB的斜率恰好等于函数f（x）在AB中点M（x0，y0）处切线的斜率？请写出判断过程．
已知函数f（x）=ax-lnx+1（a∈R），g（x）=xe1-x．
（1）求函数g（x）在区间（0，e]上的值域T；
（2）是否存在实数a，对任意给定的集合T中的元素t，在区间[1，e]上总存在两个不同的xi（i=1，2），使得f（xi）=t成立、若存在，求出a的取值范围；若不存在，请说明理由；
（3 ）函数f（x）图象上是否存在两点A（x1，y1）和B（x2，y2），使得割线AB的斜率恰好等于函数f（x）在AB中点M（x0，y0）处切线的斜率？请写出判断过程．
查看习题详情和答案>>
集合A是由适合以下性质的函数f（x）构成的：对于任意的，且u、υ∈（-1，1），都有|f（u）-f（υ）|≤3|u-υ|．
（1）判断函数f1(x)=
是否在集合A中？并说明理由；
（2）设函数f（x）=ax2+bx，且f（x）∈A，试求2a+b的取值范围；
（3）在（2）的条件下，若f（2）=6，且对于满足（2）的每个实数a，存在最小的实数m，使得当x∈[m，2]时，|f（x）|≤6恒成立，试求用a表示m的表达式．
查看习题详情和答案>>
（1）判断函数f1(x)=
| 1+x2 |
（2）设函数f（x）=ax2+bx，且f（x）∈A，试求2a+b的取值范围；
（3）在（2）的条件下，若f（2）=6，且对于满足（2）的每个实数a，存在最小的实数m，使得当x∈[m，2]时，|f（x）|≤6恒成立，试求用a表示m的表达式．
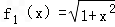是否在集合A中？并说明理由；
(a，b为实常数)．