题目内容
集合A是由适合以下性质的函数f(x)构成的:对于任意的,且u、υ∈(﹣1,1),都有|f(u)﹣f(υ)|≤3|u﹣υ|.
(1)判断函数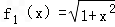 是否在集合A中?并说明理由;
是否在集合A中?并说明理由;
(2)设函数f(x)=ax2+bx,且f(x)∈A,试求2a+b的取值范围;
(3)在(2)的条件下,若f(2)=6,且对于满足(2)的每个实数a,存在最小的实数m,使得当x∈[m,2]时,|f(x)|≤6恒成立,试求用a表示m的表达式.
(1)判断函数
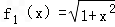 是否在集合A中?并说明理由;
是否在集合A中?并说明理由;(2)设函数f(x)=ax2+bx,且f(x)∈A,试求2a+b的取值范围;
(3)在(2)的条件下,若f(2)=6,且对于满足(2)的每个实数a,存在最小的实数m,使得当x∈[m,2]时,|f(x)|≤6恒成立,试求用a表示m的表达式.
解:(1)f1(x)∈A,任取u、υ∈(﹣1,1),且u≠υ,则
因为|u|< ,|υ|<
,|υ|<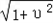 ,且|u+υ|≤|u|+|υ|
,且|u+υ|≤|u|+|υ|
所以 <1
<1
所以|f1(u)﹣f1(2)|<|u﹣υ|<3|u﹣υ|,亦即f1(x)∈A
(2)因为f(x)=ax2+bx属于集合A,所以,任取u、υ∈(﹣1,1)且u≠υ,
则3|u﹣υ|≥|f(u)﹣f(υ)|=|(u﹣υ)(au+aυ+b)|,也即|au+aυ+b|≤3 ①
设t=u+υ,则上式化为|at+b|≤3②
因为u,υ∈(﹣1,1),所以﹣2<t<2
①式对任意的u,υ∈(﹣1,1)恒成立,即②式对t∈(﹣2,2)恒成立可以证明|2a|+|b|≤3,所以|2a+b|≤3,
即2a+b∈[﹣3,3]
(3)由f(2)=6可知2a+b=3
又由(2)可知﹣3≤2a+b≤3,所以 ,
,
当a=0时,b=3,f(x)=3x在[m,2]上为单调递增函数,f(m)=3m,f(2)=4
令3m=﹣6,可得m=﹣2
当a>0时, .
.
此时,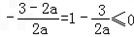 ,
,
且当x∈R时f(x)的最小值为
若 ,即
,即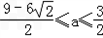 时,m为方程f(x)=6的较小根,
时,m为方程f(x)=6的较小根,
所以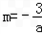
若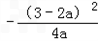 <﹣6,即0<a<
<﹣6,即0<a<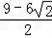 时,
时,
由于f(x)在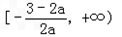 上单调递增,
上单调递增,
所以m为方程f(x)=﹣6的较大根,所以 ,
,
综上可知,m=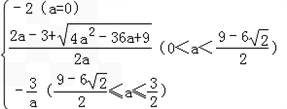

因为|u|<
 ,|υ|<
,|υ|<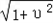 ,且|u+υ|≤|u|+|υ|
,且|u+υ|≤|u|+|υ|所以
 <1
<1所以|f1(u)﹣f1(2)|<|u﹣υ|<3|u﹣υ|,亦即f1(x)∈A
(2)因为f(x)=ax2+bx属于集合A,所以,任取u、υ∈(﹣1,1)且u≠υ,
则3|u﹣υ|≥|f(u)﹣f(υ)|=|(u﹣υ)(au+aυ+b)|,也即|au+aυ+b|≤3 ①
设t=u+υ,则上式化为|at+b|≤3②
因为u,υ∈(﹣1,1),所以﹣2<t<2
①式对任意的u,υ∈(﹣1,1)恒成立,即②式对t∈(﹣2,2)恒成立可以证明|2a|+|b|≤3,所以|2a+b|≤3,
即2a+b∈[﹣3,3]
(3)由f(2)=6可知2a+b=3
又由(2)可知﹣3≤2a+b≤3,所以
 ,
,当a=0时,b=3,f(x)=3x在[m,2]上为单调递增函数,f(m)=3m,f(2)=4
令3m=﹣6,可得m=﹣2
当a>0时,
 .
.此时,
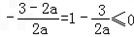 ,
,且当x∈R时f(x)的最小值为

若
 ,即
,即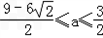 时,m为方程f(x)=6的较小根,
时,m为方程f(x)=6的较小根,所以
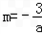
若
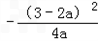 <﹣6,即0<a<
<﹣6,即0<a<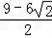 时,
时,由于f(x)在
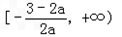 上单调递增,
上单调递增,所以m为方程f(x)=﹣6的较大根,所以
 ,
,综上可知,m=
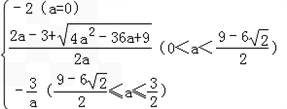

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目