摘要:(注意:在以下甲.乙两题中任选一题作答.如果两题都作答.只以甲题记分.本小题满分12分) (甲)如图,已知正四棱锥S-ABCD.底面的中心O为坐标原点.建立空间直角坐标系O-xyz.其中Ox//BC.Oy//AB.四棱锥的底面的边长为4.高为6.点M是高SO的中点.G是侧面△SBC的重心.求 (Ⅰ)MG两点间的距离, (Ⅱ)异面直线MG与BS所成的角. (乙)如图.三棱锥P-ABC中.△ABC是正三角形.∠PCA=90°.D为PA的中点.二面角P-AC-B为120°.PC = 2.AB=2. (Ⅰ)求证:AC⊥BD, (Ⅱ)求BD与底面ABC所成角的正弦值.
网址:http://m.1010jiajiao.com/timu3_id_4464483[举报]
(考生注意:本题请从以下甲乙两题中任选一题作答,若两题都答只以甲题计分)
甲:设数列{bn}的前n项和为Sn,且bn=2-Sn;数列{an} 为等差数列,且a5=9,a7=13.
(Ⅰ)求数列 {bn} 的通项公式;
(Ⅱ)若cn=anbn(n=1,2,3,…),Tn为数列{cn}的前n项和,求Tn.
乙:定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,f(x)=
-
(a∈R)
(Ⅰ)求f(x)在[0,1]上的最大值;
(Ⅱ)若f(x)是[0,1]上的增函数,求实数a的取值范围.
查看习题详情和答案>>
甲:设数列{bn}的前n项和为Sn,且bn=2-Sn;数列{an} 为等差数列,且a5=9,a7=13.
(Ⅰ)求数列 {bn} 的通项公式;
(Ⅱ)若cn=anbn(n=1,2,3,…),Tn为数列{cn}的前n项和,求Tn.
乙:定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,f(x)=
| 1 |
| 4x |
| a |
| 2x |
(Ⅰ)求f(x)在[0,1]上的最大值;
(Ⅱ)若f(x)是[0,1]上的增函数,求实数a的取值范围.
(本小题满分12分)(考生注意:本题请从以下甲乙两题中任选一题作答,若两题都答 只以甲题计分)
甲:设数列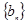 的前
的前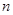 项和为
项和为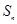 ,且
,且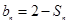 ;数列
;数列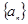 为等差数列,且
为等差数列,且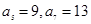
(Ⅰ)求数列 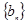 的通项公式
的通项公式
(Ⅱ)若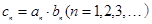 ,
, 为数列
为数列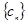 的前
的前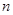 项和,求
项和,求
乙:定义在[-1,1]上的奇函数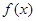 ,已知当
,已知当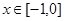 时,
时,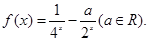
(Ⅰ)求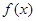 在[0,1]上的最大值
在[0,1]上的最大值
(Ⅱ)若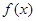 是[0,1]上的增函数,求实数
是[0,1]上的增函数,求实数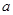 的取值范围
的取值范围
查看习题详情和答案>>
(本小题满分12分)(考生注意:本题请从以下甲乙两题中任选一题作答,若两题都答 只以甲题计分)
只以甲题计分)
甲:设数列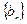 的前
的前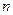 项和为
项和为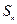 ,且
,且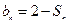 ;数列
;数列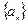 为等差数列,且
为等差数列,且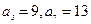
(Ⅰ)求数列 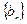 的通项公式
的通项公式
(Ⅱ)若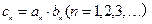 ,
,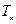 为数列
为数列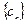 的前
的前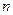
 项和,求
项和,求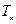
乙:定义在[-1,1]上的奇函数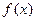 ,已知当
,已知当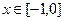 时,
时,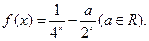
(Ⅰ)求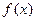 在[0,1]上的最大值
在[0,1]上的最大值
(Ⅱ)若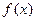 是[0,1]上的增函数,求实数
是[0,1]上的增函数,求实数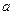 的取值范围
的取值范围
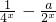 (a∈R)
(a∈R)